Última alteração: Junho 13, 2002

BACHARELADO EM CIÊNCIA DA COMPUTAÇÃO (BCC) E MATEMÁTICA COMPUTACIONAL (BMC)
ALGORITMOS E ESTRUTURAS DE DADOS III
Professores: Nivio Ziviani (BCC) e Wagner Meira Jr (BMC)
Monitores: Robert Pereira Pinto e Fabricio Benevenuto de Souza
Trabalho Prático 1
Data de Entrega: 28-Junho-2002

1.
Avaliar as somas (1 + 1 + 1 pontos):
(a)
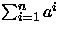
\(\sum_{i=1}^n a^i\)
(b)
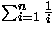
\(\sum_{i=1}^n \frac{1}{i}\)
(c)
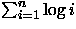
\(\sum_{i=1}^n \log i\)
2.
Apresente a complexidade de tempo para os procedimentos abaixo: 1 + 1 + 1 pontos)

(a) 
      PROCEDURE Pesquisa ( n : integer);
      BEGIN
        IF n > 1
        THEN BEGIN
             Inspecione n*n elementos;
             Pesquisa (2n/3);
             END;
      END;
(b) 
      PROCEDURE Sort ( VAR A: ARRAY[1..n] OF integer;
                       i, j: integer );
      { n uma potencia de 2 }
      BEGIN
        IF i < j
        THEN BEGIN
             m := (i + j - 1)/2;
             Sort(A,i,m);
             Sort(A,m+1,j);
             Merge(A,i,m,j);
             { Merge intercala A[i..m] e A[m+1..j] em A[i..j] }
             END;
      END;

(c) 
      PROCEDURE Proc ( n : integer);
      BEGIN
        IF n = 0 THEN RETURN 1
                 ELSE RETURN T(n-1) + T(n-1)
      ENDE;

3.
Árvore de Pesquisa (1 + 1 + 1 pontos) 
      PROCEDURE Pesquisa (ChavePesq: Integer; VAR p: Apontador);
      BEGIN 
        IF p = nil
        THEN writeln(' Erro: Registro nao esta' presente na arvore')
        ELSE IF ChavePesq < p^.Reg.Chave 
             THEN Pesquisa (ChavePesq, p^.Esq)
             ELSE IF ChavePesq > p^.Reg.Chave
                  THEN Pesquisa (ChavePesq, p^.Dir)
                  ELSE Encontrou o registro;
      END;

(a)
Mostre analiticamente o melhor caso, o pior caso e o caso esperado para o número de comparações em uma pesquisa com sucesso;
(b)
Determine empiricamente o número esperado de comparações em uma pesquisa com sucesso;
(c)
compare os resultados obtidos no item (b) com resultados analíticos obtidos.

Utilize o procedimento Permut abaixo para obter uma permutacao randômica das chaves. 

#include <stdio.h>
#include <stdlib.h>
#include <sys/types.h>
#include <sys/timeb.h>

void IniciaRand() { /* Substituir por uma funcao que tome tempo em ms */
  time_t ltime;
  time(&ltime);
  ltime%=10000;
  srand(ltime);
}

double rand0a1() {
  double resultado=  (double) rand()/ 0x7FFF; /* Dividir pelo maior inteiro */
  if(resultado>1.0) resultado= 1.0;
  return resultado;
}

void Permut( int A[], int n) {
 int i,j,b;

 IniciaRand(); /* Funcao que Inicia a geracao de numeros randomicos */
 for(i = n-1; i>0; i --) {
   j = (i * rand0a1()) +1 ;
   b = A[i];
   A[i] = A[j];
   A[j] = b;
 }
}

int main() {
  unsigned int x;
  int v[20];

  for(x=0;x<20;x++)    v[x]=x;
  Permut(v,20);
  for(x=0;x<20;x++)  printf("%d ",v[x]);
  printf("\n");
  return 0; 
}

4.
Unificação de Listas (2 + 0,5 + 0.5 + 0.5 pontos)

O problema da unificação da lista aparece na codificação de Huffman, um método estatístico para compressão de textos (ou dados em geral). A codificação de Huffman atribui um código de tamanho fixo para cada símbolo (símbolo pode ser um caractere ou uma palavra) diferente do texto. A compressão é obtida através da atribuição de um número menor de bits para símbolos com maior probabilidade de ocorrência no texto. A principal etapa na construção da árvore de Huffman é a unificação da lista ordenada contendo a frequência de ocorrência de cada símbolo no texto.

Dada uma lista ordenada de n elementos de valor inteiro, o problema de unificação da lista consiste em realizar seguidamente a operação de remover os dois elementos de menor valor da lista e inserir um novo elemento com valor igual a soma dos dois primeiros. A cada operação realizada a lista passa a ter um elemento a menos. A unificação termina quando restar somente um elemento na lista.

Exemplo: A unificação da lista {20,40,50,70,80} teria os passos intermediários {50,60,70,80}, {70,80,110}, {110,150} e {260}

(a)
Implemente um algoritmo que realize a unificação da lista em tempo linear (O(n)). Apresente uma descrição do algoritmo e das estruturas de dados utilizadas. A listagem da implementação deve ser entregue e o programa submetido (veja aqui maiores detalhes sobre instruções para a entrega de trabalhos praticos).
(b)
Apresente a análise de complexidade do seu algoritmo.

(c)
É possível realizar a unificação em tempo sublinear ? Justifique a sua resposta.

(d)
Qual o limite inferior para o problema da unificação ?

Observação: A resposta do item b só terá validade se a justificativa para a resposta apresentar argumentos convincentes.


Nivio Ziviani
6/13/2002