Algoritmos de ordenação parcial: estudos comparativos
(1,5 + 1,5 + 1,5 + 0,5 pontos)
O problema da ordenação parcial ocorre quando se deseja obter
os 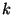 primeiros elementos de um arranjo contendo
primeiros elementos de um arranjo contendo 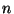 elementos,
em uma ordem ascendente ou descendente.
Quando
elementos,
em uma ordem ascendente ou descendente.
Quando 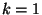 o problema se reduz a encontrar o mínimo
(ou o máximo) de um conjunto de elementos.
Quandfo
o problema se reduz a encontrar o mínimo
(ou o máximo) de um conjunto de elementos.
Quandfo 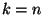 caimos no problema clássico de ordenação.
caimos no problema clássico de ordenação.
O problema da ordenação parcial ocorre em muitas situações
práticas (Barbosa, 2003).
Por exemplo, para facilitar a busca de informação na Web existem
as máquinas de busca,
que são sistemas para recuperação de informação na Web
(Baeza-Yates e Ribeiro-Neto, 1999; Witten, Mofat e Bell, 1999)
É comum uma consulta na Web retornar centenas de milhares de
documentos relacionados com a consulta.
Entretanto, o usuário está interessado apenas nos 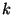 documentos
mais relevantes, onde
documentos
mais relevantes, onde 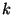 , em geral, é menor do que 200 documentos
(na realidade o usuário consulta apenas os 10 primeiros documentos
mostrados na primeira página de resposta na maioria das vezes).
Consequentemente, a comunidade de recuperação de informação
necessita de algoritmos eficientes de ordenação parcial.
, em geral, é menor do que 200 documentos
(na realidade o usuário consulta apenas os 10 primeiros documentos
mostrados na primeira página de resposta na maioria das vezes).
Consequentemente, a comunidade de recuperação de informação
necessita de algoritmos eficientes de ordenação parcial.
O objetivo deste trabalho é realizar um estudo comparativo dos
principais algoritmos de ordenação interna que possam ser
adaptados para realizar eficientemente ordenação parcial.
Assim, considere os seguintes algoritmos de ordenação
interna: Inserção, Shellsort, Heapsort, Quicksort (Ziviani, 1993).
- Determine experimentalmente o número esperado de (i) comparações
e (ii) movimento-de-registros para cada um dos métodos de
ordenação indicados acima.
Utilize arquivos de diferentes tamanhos com chaves geradas randomicamente.
Use o programa Permut.c apresentado abaixo para obter uma
permutação randômica de 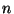 valores.
Repita
cada experimento algumas vezes e obtenha a média para cada medida
de complexidade.
Dê a sua interpretação dos dados obtidos,
comparando-os com resultados analíticos.
valores.
Repita
cada experimento algumas vezes e obtenha a média para cada medida
de complexidade.
Dê a sua interpretação dos dados obtidos,
comparando-os com resultados analíticos.
- Uma opção alternativa
é considerar os mesmos algoritmos propostos e determinar
experimentalmente o tempo de execução de cada um dos
métodos de ordenação indicados acima.
Use o programa Permut.c para gerar arquivos de
tamanhos 1.000, 10.000, 100.000 e 1.000.000 de registros.
Para cada tamanho de arquivo
dê a sua interpretação dos dados obtidos.
- Apresente resultados analíticos para os algoritmos estudados.
Considere diferentes valores de
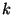 , tais como
, tais como 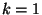 ,
, 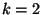 ,
,
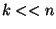 , e
, e 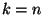 , onde o caso
, onde o caso 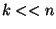 é o mais interessante.
é o mais interessante.
- Procure trabalhos relacionados na literatura (se houver)
que tratem do assunto e descreva suscintamente esses trabalhos.
Observações:
- Utilize o procedimento Permut.c abaixo para obter uma permutacao
randômica das chaves.
#include <stdio.h>
#include <stdlib.h>
#include <sys/types.h>
#include <sys/timeb.h>
void IniciaRand() { /* Substituir por uma funcao que tome tempo em ms */
time_t ltime;
time(<ime);
ltime%=10000;
srand(ltime);
}
double rand0a1() {
double resultado= (double) rand()/ 0x7FFF; /* Dividir pelo maior inteiro */
if(resultado>1.0) resultado= 1.0;
return resultado;
}
void Permut( int A[], int n) {
int i,j,b;
IniciaRand(); /* Funcao que Inicia a geracao de numeros randomicos */
for(i = n-1; i>0; i --) {
j = (i * rand0a1()) +1 ;
b = A[i];
A[i] = A[j];
A[j] = b;
}
}
int main() {
unsigned int x;
int v[20];
for(x=0;x<20;x++) v[x]=x;
Permut(v,20);
for(x=0;x<20;x++) printf("%d ",v[x]);
printf("\n");
return 0;
}
- O problema da ordenação parcial foi proposto por
Barbosa (2003).
[BYR] R. Baeza-Yates and B. Ribeiro-Neto
Modern Information Retrieval,
Addison-Wesley, 1999.
Ramurti A. Barbosa Comunicação pessoal, Akwan Information Technologies, 2003.
[WMB99] I. H. Witten, A. Moffat, T.C. Bell Managing Gigabytes Compressing
and Indexing Documents and Images, Morgan Kaufmann Publishers, 1999 (second
edition). Bom livro sobre implementação de sistemas de RI.
[Z] Ziviani, N. Projeto de Algoritmos Com
Implementações em Pascal e C,
Pioneira Thomson Learning, 1993.

