Considere
a soma da série (o que queremos avaliar), então temos:
Departamento de Ciência da Computação
Universidade Federal de Minas Gerais
Belo Horizonte -- Brasil
| Aluno: | Adriano César Machado Pereira |
| E-mail: | adrianoc@dcc.ufmg.br |
| Data: | 16/Maio/2003 |
a)
Considere a soma da série (o que queremos avaliar), então temos:
, temos:
por , temos:
em evidência, temos:
, que é a soma buscada, obtemos:
.
temos a solução trivial 
, obtida a partir da soma do valor 
que ocorre 
vezes.
tendendo a infinito, a série converge somente quando 
, fazendo com que a soma vá converter para
.
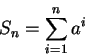
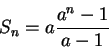
b)
De acordo com Cormen [5], para inteiros positivos , o -ésimo número harmônico é:
, que gera como resultado: 
 |
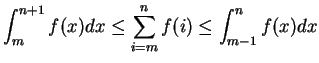(1) | ||
 |
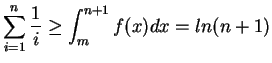(2) |
 |
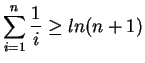(3) |
 |
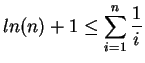(4) |
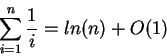
c)
Considere a soma da série (o que queremos avaliar), então temos:
, temos:
como
.
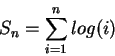
1)
Pesquisa(n);
if n <= 1
then termine
else begin
obtenha o maior elemento dentre os n elementos;
{de alguma forma isto permite descartar 2/5 dos}
{elementos e fazer uma chamada recursiva no resto}
Pesquisa(3n/5);
end;
Podemos escrever a fórmula de recorrência analisando o caso base,
quando 
então 
e no caso para 
então
. Dessa forma, temos que:
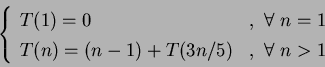
A cada iteração, são descartados 
de . No caso de 
iterações temos que a condição de parada seja
 |
 |
 |
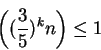
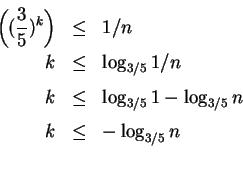
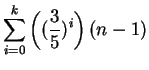(5) |
|
|
 |
para o caso em que .
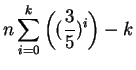Fazendo um ajuste no somatório para que 
inicie com valor 1 e resolvendo esse somatório encontramos o seguinte resultado:
|
|
 |
2)
FUNCTION Fib(n: integer): integer;
BEGIN
IF n = 0
THEN Fib := 0
ELSE IF n = 1
THEN Fib := 1
ELSE Fib := Fib(n-1) + Fib(n-2)
END;
A função acima, denominada sequência de Fibonacci, pode ser expressa através de uma relação de recorrência de segunda ordem, de acordo com Grossman [6]:
A fim de solucionar essa equação, podemos supor uma solução exponencial do tipo 
e
substituímos na relação para encontrar a equação característica. Assim, temos:
Dividindo a equação por 
e passando os termos para o lado esquerdo,
encontramos a equação característica
. Agora basta resolver essa
equação do segundo grau e teremos como raízes:
e
De acordo com o teorema da combinação linear das soluções dessa equação [6], a solução geral obtida é da forma:
.
Ou seja, em nosso caso seria:
Agora basta utilizar os valores da condições iniciais fornecidas para se determinar os valores de 
e 
:
Portanto a solução desse sistema é:
e
Conclui-se então que a solução para os termos da sequência Fibonacci é a seguinte:
3)
PROCEDURE Sort1 ( VAR A: ARRAY[1..n] OF integer;
i, j: integer ); { n uma potencia de 2 }
BEGIN
IF i < j
THEN BEGIN
m := (i + j - 1)/2;
Sort1(A,i,m);
Sort1(A,m+1,j);
Merge(A,i,m,j);
{Merge intercala A[i..m] e A[m+1..j] em A[i..j] }
END;
END;
Esse algoritmo realiza os seguintes passos de maneira recursiva:
comparações no pior caso.
, o custo
do 2º Sort = e o custo do Merge = no pior
caso, podemos obter a seguinte relação de recorrência:
:
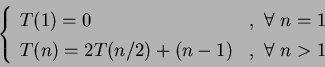
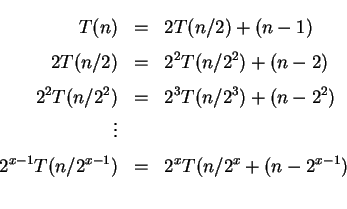
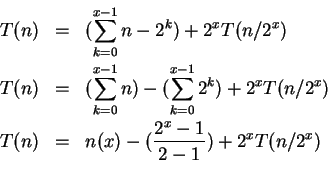
Considerando 
temos que:
4)
PROCEDURE Sort2 ( VAR A: ARRAY[1..n]OF integer;
i, j: integer );
{ n uma potencia de 3 }
BEGIN
IF i < j
THEN BEGIN
m := ( (j - i) + 1 )/3;
Sort2(A,i,i+m-1);
Sort2(A,i+m,i+ 2m -1);
Sort2(A,i+2m,j);
Merge(A,i,i+m,i+2m, j);
{ Merge intercala A[i..(i+m-1)], A[(i+m)..(i+2m-1) e
A[i+2m..j] em A[i..j] a um custo ( (5n/3) -2 ) }
END;
END;
Esse algoritmo realiza os seguintes passos de maneira recursiva:
comparações no pior caso.
, o custo
do 2º Sort = , o custo do 3º Sort = ,
e o custo do Merge = no pior
caso, podemos obter a seguinte relação de recorrência:
:
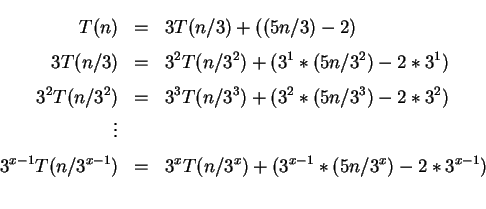
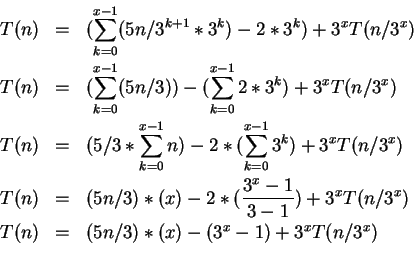
Considerando 
temos que: 
Portanto a complexidade desta relação de recorrência é da forma:
.
A análise da complexidade envolve o problema de se estabelecer um limite inferior para essa classe de algoritmos que se baseiam em comparação entre chaves. Ao obter esse limite torna-se mais intuitivo a análise de desempenho desses algoritmos.
A demonstração formal exige inicialmente definirmos um modelo denominado Árvore de Decisão. Uma Árvore de Decisão é uma árvore binária completa que representa as comparações executadas por um algoritmo de ordenação quando ele opera sobre uma entrada de um determinado tamanho conhecido. A execução do algoritmo de ordenação corresponde a determinar um caminho desde a raiz da árvore de decisão até uma folha. Em cada nó interno é feita uma comparação, sendo que a subárvore determina as comparações subsequentes. Quando se chegaa uma folha, o algoritmo de ordenação estabelece a ordem
. Como qualquer algoritmo de ordenação deve ser capaz de produzir cada permutação de sua entrada, então para que uma ordenação por comparação seja correta é necessário que cada uma das 
permutações sobre elementos apareçam como uma das folhas da árvore de decisão, e que cada uma dessas folhas sejam acessíveis a partir da raiz por um caminho correspondente a um execução real da ordenação por comparação [5].
O problema inicial consiste em achar um árvore de decisão que minimize o número máximo de comparações feitas, ou seja, o comprimento do caminho mais longo da raiz de uma árvore de decisão até qualquer de suas folhas acessíveis, que representa o número de comparações para o pior caso que o algorimo de ordenação correspondente executa. Logo devemos determinar a altura da árvore, conforme descrito em [5,8].
A fim de obter a altura de uma árvore de decisão em que cada permutação aparece como uma folha acessível basta considerarmos 
como a altura e 
como folhas acessíveis e teremos que cada permutações da entrada aparece como uma folha, logo obtemos 
. Comouma árvore binária de altura não possui mais que 
folhas, logo temos que
Dessa forma, podemos escrever a inequação anterior utilizando as propriedades de logaritmos da seguinte forma:
comparações no pior caso. primeiros elementos de um arranjo contendo elementos, em uma ordem ascendente ou descendente. Quando 
o problema se reduz a encontrar o mínimo (ou o máximo) de um conjunto de elementos. Quando 
caimos no problema clássico de ordenação.
O problema da ordenação parcial ocorre em muitas situações práticas [4]. Por exemplo, para facilitar a busca de informação na Web existem as máquinas de busca, que são sistemas para recuperação de informação na Web [3,9] é comum uma consulta na Web retornar centenas de milhares de documentos relacionados com a consulta. Entretanto, o usuário está interessado apenas nos documentos mais relevantes, onde , em geral, é menor do que 200 documentos (na realidade o usuário consulta apenas os 10 primeiros documentos mostrados na primeira página de resposta na maioria das vezes). Consequentemente, a comunidade de recuperação de informação necessita de algoritmos eficientes de ordenação parcial.
O objetivo deste trabalho foi realizar um estudo comparativo dos principais algoritmos de ordenação interna que possam ser adaptados para realizar eficientemente ordenação parcial. Aprincípio foi solicitado considerar os seguintes algoritmos de ordenação interna: Inserção, Shellsort, Heapsort, Quicksort [10].
Hoje em dia há várias situações que demandam a ordenação de apenas um
subconjunto de elementos dentre seu conjunto total. Nesses casos, ordenar
um vetor e listar apenas os primeiros termos requer trabalho extra,
já que os algoritmos estudados de ordenação ordenam totalmente o vetor.
A solução trivial para esse tipo de problema é bem simples, sendo que
consiste em aplicar um algoritmo de busca por comparação entre chaves (Quicksort, por exemplo) e, após ordenado o vetor, listar apenas os primeiros elementos. Nesse trabalho prático, implementou-se novas versões desses algoritmos para o problema da Ordenação Parcial e as discussões e resultados obtidos são apresentados nas questões 1 a 4 que se seguem. Decidiu-se por não alterar o Shellsort, uma vez que ele é uma variação do algoritmo de inserção e sua análise de complexidade não é conhecida.
Observação: Utilize arquivos de diferentes tamanhos com chaves geradas randomicamente. Use o programa Permut.c apresentado abaixo para obter uma permutação randômica de valores. Repita cada experimento algumas vezes e obtenha a média para cada medida de complexidade. Dê a sua interpretação dos dados obtidos, comparando-os com resultados analíticos.
Inicialmente gostaria de ressaltar que vou apresentar os algoritmos que criei baseados nos algoritmos de ordenação por inserção, seleção, Quicksort, Heapsort e outra versão do Quicksort que encontrei para o problema da ordenação parcial. Mas gostaria de fazer algumas observações sobre o algoritmo Shellsort a seguir.
Criado por Donald L. Shell em 1959, o Shellsort é apenas uma extensão do algoritmo da inser ção direta. Esta extensão resume-se a dar um valor de salto para o teste de inserção. O Shellsort apresenta ótimos resultados para arquivos de tamanho moderado.
Para o problema de Ordenação Parcial, o Shellsort também seria adequado para arquivos de tamanho moderado, e a sua solução seria a trivialmente obtida. Neste trabalho o objetivo é obter eficiência na ordenação parcial, portanto optei por não utilizá-lo. Além disso, existe a impossibilidade de se analisar a complexidade de tempo desse algoritmo, o que tornaria inviável a minha análise, uma vez que é desconhecida a razão pela qual o Shellsort é eficiente[10].
Não foi possível alterar esse algoritmo de forma a otimizá-lo para o problema em questão, sem que sua essência fosse modificada.
O algoritmo de ordenação por inserção é bastante simples e eficiente para uma quantidade pequena de números. A idéia de funcionamento é semelhante ao ordenamento de cartas de baralho na mão de um jogador. A mão esquerda começa vazia e a mão direita insere uma carta de cada vez na posição correta. Ao final, quando todas as cartas foram inseridas, elas já estão ordenadas. Para encontrar, durante a inserção, a posição correta para um valor, compara-se este valor um-a-um com as cartas já na mão esquerda, até encontrarmos a posição correta.
Neste algoritmo não há necessidade de utilização de nenhuma estrutura de dados extra, além do próprio vetor inicial com os valores. Considere que os números a serem ordenados estão armazenados num vetor. O algoritmo de ordenação por inserção tem complexidade proporcional a 
no pior caso, onde n é o número de elementos a serem ordenados. O código do algoritmo para ordenação por inserção pode ser obtido em [10,5].
A fim de atender ao problema de ordenação parcial alterei o algoritmo para que fossem desconsiderados os elementos maiores que o k-ésimo elemento já ordenado. Assim, o algoritmo de ordenação parcial ficou da seguinte maneira:
void InsercaoParcial(Vetor A, Indice k)
{
Indice i, j;
Item x;
for (i = 2; i <= n; i++) {
x = A[i];
if (i > k) { // Alteração realizada para evitar comparação com
j = k; // elementos maiores que o k-ésimo elemento.
}
else {
j = i - 1;
}
A[0] = x; /* sentinela */
numComparacoes++;
while (x.Chave < A[j].Chave) {
A[j + 1] = A[j];
numMovimentacoes++;
j--;
numComparacoes++;
}
if ( i <= k){
A[j + 1] = x;
numMovimentacoes++;
}else if (j != k){ // Alteração realizada para ordenação dos
A[j + 1] = x; // k-ésimos ser feita corretamente.
numMovimentacoes++;
} // if
} // for
} /* Insercao Parcial */
A tabela 1 ilustra o número esperado de comparações do algoritmo de inserção parcial implementado. Esses valores foram coletados experimentalmente, executando vários testes com o algoritmo, que foi instrumentado,obtendo posteriormente a média de comparações entre chaves.
A tabela 2 ilustra o número esperado de movimento de registros do algoritmo de inserção parcial implementado. Esses valores foram coletados experimentalmente, executando vários testes com o algoritmo, que foi instrumentado,obtendo posteriormente a média de movimentações.
O método de ordenação por Seleção Direta é levemente mais eficiente que o método Bubblesort, ainda que se trate de um algoritmo apenas para ordenação de pequenos arranjos.
A lógica consiste em se varrer o arranjo comparando todos os seus elementos com o primeiro. Caso o primeiro elemento esteja desordenado em relação ao elemento que está sendo comparado com ele no momento, então é feita a troca. Ao se chegar ao final do arranjo, teremos o menor valor na primeira posição do arranjo.
Este primeiro passo nos garante que o menor elemento fique na primeira posição. Continuamos, assim, a varrer os demais elementos, comparando-os com a segunda posição do arranjo (já desconsiderando a primeira posição, que foi anteriormente ordenada em relação ao arranjo como um todo).
O algoritmo original da Seleção tem ordem de complexidade igual a 
,
pois para cada um dos elementos a serem ordenados, necessita-se de uma
busca nos elementos restantes, a menos daqueles que já estão ordenados.
A alteração realizada, reduz a função assintótica para 
para valores
de k menores do que n, onde normalmente 
.
O algoritmo de seleção parcial que implementei é bem parecido com o original. Nessa versão modificada apenas modifiquei de por no anel mais externo para iterar somente sobre os primeiros elementos. O código do algoritmo de ordenação por seleção parcial é apresentado a seguir:
(k=1%n)
void SelecaoParcial (Vetor A, Indice k)
{
Indice i, j, Min;
Item x;
for (i = 1; i < (k+1); i++) { // Alteracao realizada para
Min = i; // pegar só k elementos
for (j = i + 1; j <= n; j++) {
numComparacoes++;
if (A[j].Chave < A[Min].Chave) {
Min = j;
}
}
x = A[Min];
A[Min] = A[i];
numMovimentacoes++;
A[i] = x;
numMovimentacoes++;
}
} /* Selecao Parcial */
A tabela 3 ilustra o número esperado de comparações do algoritmo de seleção parcial implementado. Esses valores foram coletados experimentalmente, executando vários testes com o algoritmo, que foi instrumentado,obtendo posteriormente a média de comparações entre chaves.
A tabela 4 ilustra o número esperado de movimento de registros do algoritmo de seleção parcial implementado. Esses valores foram coletados experimentalmente, executando vários testes com o algoritmo, que foi instrumentado,obtendo posteriormente a média de movimentações.
elementos em dois problemas menores e idênticos. Para isso é escolhido um elemento, que chamamos de pivô. Esse pivô particiona o conjunto em dois: um com os elementos menores do que ele e outro com os elementos maiores. A partir desse ponto, o algoritmo é executado recursivamente nas duas partições geradas.
A otimização que foi proposta para o problema da ordenação parcial consiste em podar o conjunto, desprezando todos os elementos maiores do que o -ésimo elemento. Sendo assim, há três possíveis situações, que podem ocorrer de acordo com a escolha do pivô:
e outra com os elementos restantes. Sendo assim, não é
possível prosseguir com a ordenação parcial só nesse subconjunto de valores menores
do que o pivô, uma vez que existirão elementos de interesse na outra partição de elementos maiores do que o pivô. Se isso ocorrer, o algoritmo original é executado.
e outra com os 
restantes, que são maiores que o pivô.
Se isso ocorre, basta desprezar a partição dos elementos maiores, pois os
elementos de interesse (k) já estão na partição de elementos menores, considerando
também o pivô. Vale ressaltar que essa situação consiste do caso ótimo para a
ordenação parcial utilizando esse algoritmo.
e outra com os elementos restantes. Se isso ocorre,
basta desprezarmos o conjunto de elementos maiores que o pivô e as outras chamadas
recursivas continuarão podando o vetor que se quer ordenar.
O código do algoritmo Quicksort parcial implementado é apresentado a seguir:
void Particao(Vetor A, Indice Esq, Indice Dir, Indice *i, Indice *j)
{
Item x, w;
*i = Esq;
*j = Dir;
x = A[(*i + *j) / 2]; /* obtem o pivo x */
do {
numComparacoes++;
while (A[*i].Chave < x.Chave){
(*i)++;
numComparacoes++;
}
numComparacoes++;
while (A[*j].Chave > x.Chave){
(*j)--;
numComparacoes++;
}
if (*i <= *j) {
w = A[*i];
A[*i] = A[*j]; numMovimentacoes++;
A[*j] = w; numMovimentacoes++;
(*i)++;
(*j)--;
}
} while (*i <= *j); /* Particao */
}
void Ordena(Vetor A, Indice Esq, Indice Dir, Indice k)
{
Indice i, j;
Particao(A, Esq, Dir, &i, &j);
/* Otimizacao */
if ( (j - Esq) >= (k-1) ){
if (Esq < j)
Ordena(A, Esq, j, k);
}else{
if (Esq < j)
Ordena(A, Esq, j, k);
if (i < Dir)
Ordena(A, i, Dir, k);
}
} /* Ordena */
void QuicksortParcial(Vetor A, Indice k)
{
Ordena(A, 1, n, k);
} /* Quicksort */
A tabela 5 ilustra o número esperado de comparações do algoritmo Quicksort parcial implementado. Esses valores foram coletados experimentalmente, executando vários testes com o algoritmo, que foi instrumentado,obtendo posteriormente a média de comparações entre chaves.
A tabela 6 ilustra o número esperado de movimento de registros do algoritmo Quicksort parcial implementado. Esses valores foram coletados experimentalmente, executando vários testes com o algoritmo, que foi instrumentado,obtendo posteriormente a média de movimentações.
Heapsort é um método de ordenação cujo princípio de funcionamento é o mesmo utilizado para a ordenação por seleção, a saber:
O custo para encontrar o menor (ou o maior) item entre n itens custa n-1 comparações. Esse custo pode ser reduzido através da utilização de uma estrutura de dados denominada fila de prioridades [10].
O algoritmo Heapsort parcial implementado foi elaborado invertendo inicialmente a construção do Heap. Para isso alterei a função Refaz do algoritmo fornecido pelo livro [10]. Dessa forma os elementos de menor valor foram sendo colocados no topo da pilha, possibilitando refazer a pilha somente até o k-ésimo elemento.
O código do algoritmo Heapsort parcial implementado é apresentado a seguir:
void Refaz(Indice Esq, Indice Dir, Vetor A)
{
Indice i;
int j;
Item x;
i = Esq;
j = i * 2;
x = A[i];
while (j <= Dir) {
numComparacoes++;
if (j < Dir) {
if (A[j].Chave >= A[j + 1].Chave){ // Alteracao realizada para construir
// o heap de maneira invertida
j++;
}
}
numComparacoes++;
if (x.Chave < A[j].Chave){ // Alteracao realizada para construit
// o heap de maneira invertida
goto LABEL;
}
A[i] = A[j];
numMovimentacoes++;
i = j;
j = i * 2;
}
LABEL:
A[i] = x;
numMovimentacoes++;
} /* Refaz */
void HeapsortParcial(Vetor A, Indice k)
{
Indice Esq, Dir;
Item x;
int aux = 0; // Alteracao 3 - variável que controla a posição
// no heap invertido
/* constr o i o heap */
Esq = n / 2 + 1;
Dir = n;
while (Esq > 1) {
Esq--;
Refaz(Esq, Dir, A);
}
/* ordena o vetor */
while (aux < k) { // Alteracao 4 - mantêm os menores elementos
// ordenados nas posições (n - k)
x = A[1];
A[1] = A[n - aux];
A[n - aux] = x;
Dir--;
aux++;
Refaz(Esq, Dir, A);
}
} /* HeapsortParcial */
A tabela 7 ilustra o número esperado de comparações do algoritmo Heapsort parcial implementado. Esses valores foram coletados experimentalmente, executando vários testes com o algoritmo, que foi instrumentado,obtendo posteriormente a média de comparações entre chaves.
A tabela 8 ilustra o número esperado de movimento de registros do algoritmo Heapsort parcial implementado. Esses valores foram coletados experimentalmente, executando vários testes com o algoritmo, que foi instrumentado,obtendo posteriormente a média de movimentações.
O algoritmo desta subseção foi obtido em [2] e utilizado como comparação para minhas implementações realizadas. O código desse algoritmo é listado a seguir. Realizou-se as devidas instrumentações para efeitos experimentais.
void PartialQuickSort(T v[], int a, int b, int first, int last)
{
if ( ! overlap(a, b, first, last) )
return;
// caso básico (tamanho <= 1)
if (a >= b)
return;
// inicializações
T x = v[(a + b) / 2];
int i = a;
int j = b;
// passo de partição
do
{
numComparacoes++;
while (v[i] < x){
i++;
numComparacoes++;
}
numComparacoes++;
while (v[j] > x){
j--;
numComparacoes++;
}
if (i > j){
break;
}
T tmp = v[i];
v[i++] = v[j];
numMovimentacoes++;
v[j--] = tmp;
numMovimentacoes++;
} while (i <= j);
PartialQuickSort(v, a, j, first, last);
PartialQuickSort(v, i, b, first, last);
}
A tabela 9 ilustra o número esperado de comparações do algoritmo Partial Quicksort, implementação obtida em C++. Esses valores foram coletados experimentalmente, executando vários testes com esse algoritmo, que foi instrumentado,obtendo posteriormente a média de comparações entre chaves.
A tabela 10 ilustra o número esperado de movimento de registros do algoritmo Partial Quicksort, implementação obtida em C++. Esses valores foram coletados experimentalmente, executando vários testes com o algoritmo, que foi instrumentado,obtendo posteriormente a média de movimentações.
Observação: Use o programa Permut.c para gerar arquivos de tamanhos 1.000, 10.000, 100.000 e 1.000.000 de registros. Para cada tamanho de arquivo dê a sua interpretação dos dados obtidos.
A tabela 11 ilustra o tempo de execução do algoritmo de inserção parcial implementado. Esses valores foram obtidos experimentalmente, executando vários testes com o algoritmo, que foi instrumentado, obtendo posteriormente a média de tempo de execução.
A tabela 12 ilustra o tempo de execução do algoritmo de seleção parcial implementado. Esses valores foram obtidos experimentalmente, executando vários testes com o algoritmo, que foi instrumentado, obtendo posteriormente a média de tempo de execução.
A tabela 13 ilustra o tempo de execução do algoritmo Quicksort parcial implementado. Esses valores foram obtidos experimentalmente, executando vários testes com o algoritmo, que foi instrumentado, obtendo posteriormente a média de tempo de execução.
A tabela 14 ilustra o tempo de execução do algoritmo Heapsort parcial implementado. Esses valores foram obtidos experimentalmente, executando vários testes com o algoritmo, que foi instrumentado, obtendo posteriormente a média de tempo de execução.
A tabela 15 ilustra o tempo de execução do algoritmo Partial Quicksort, implementação obtida em C++. Esses valores foram obtidos experimentalmente, executando vários testes com o algoritmo, que foi instrumentado, obtendo posteriormente a média de tempo de execução.
, tais como , 
, , e , onde o caso é o mais interessante.
.
Substituindo por obteríamos a análise de complexidade apresentada em [10], ou seja:
.
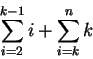
A análise de complexidade do algoritmo de seleção parcial implementado é a seguinte:
Para o caso de ser encontraremos a complexidade de tempo apresentada em [10].
A análise de complexidade do algoritmo Quicksort parcial implementado é mais complicada que os demais e requer analisar os três casos previamente descritos na subseção 4.1.4.
Já é sabido que se ao gerar o pivô se uma das partições fica vazia, então temos o pior caso possível. Nesse caso a ordem de complexidade seria da ordem de 
. Essa demonstração não é intuitiva, mas sua demonstração pode ser vista em [5]. A outra possibilidade seria o melhor caso do algoritmo implementado, onde o pivô escolhido para particionar o vetor, seria o nosso . Sendo assim a recursividade seria aplicada somente na partição onde se encontra somente os valores menores que . Essa complexidade seria da ordem de
. Mas essa situação é bem difícil de ocorrer.
Mas a situação mais provável de ocorrer é quando a partição com elementos menores que o pivô possua maior número de elementos que . E nesse caso a complexidade conhecida do QuickSort [10] é aplicada, ou seja: 
. Porém essa complexidade é aplicada somente ao conjunto de elementos menores que o pivô e as demais partições são descartadas. Sendo assim a complexidade do Quicksort parcial para esse terceiro caso é variável no intervalo que vai de
até
.
A análise de complexidade do HeapsortParcial é trivial. É sabido que a construção do Heap possui custo igual a 
. Com a alteração realizada no código, a busca para os primeiros termos é linear, logo a função Refaz é executada vezes, logo a complexidade do Heapsort Parcial é 
. Observe que no caso em que for igual a , a complexidade obtida será , já conhecida na literatura.
A fim de se concluir os aspectos mais interessantes deste trabalho, nesta seção são apresentados alguns resultados comparativos e observações dos mesmos. Vale ressaltar que todos os experimentos foram realizados em uma máquina com processador AMD ATHLON 1 GHz, com 1 GHz de memória, rodando sistema operacional Linux Debian Linux - versão 2.4.20.
As tabelas 17, 16 e 18 fazem um resumo dos resultados obtidos para vários valores de k aplicando as análises de complexidade obtidas para cada um dos algoritmos implementados, levando-se em conta o tamanho do conjunto igual a 100.000 elementos.
A análise da tabela 16 possibilitou concluir que, em termos movimentação de de chaves, o melhor algoritmo foi o Quicksort parcial implementado no trabalho. Para isso foi considerado o valor de n mais interessante, ou seja, 
.
A análise da tabela 17 possibilitou concluir que, em termos de comparação entre chaves, o melhor algoritmo foi o Quicksort parcial implementado no trabalho. Para isso foi considerado o valor de n mais interessante, ou seja, .
Porém para o problema proposto (ordenação parcial), a métrica mais importante é eficiência em termos de tempo computacional. A análise da tabela 18 demonstra que, sendo o tempo mínimo de execução o objetivo principal, o algoritmo Partial Quicksort é o que proporcionou o melhor resultado. Vale ressaltar que isso foi possível, mesmo realizando mais movimentações de chaves e comparações entre elas, devido a um passo inicial que ele executa, lhe possibilitando obter melhor elemento pivô.
Considerando diferentes valores de , tais como , , e , onde
o caso é o mais interessante, podemos descrever a complexidade, como pode ser visto
na tabela 19.
Vale ressaltar que o algoritmo Quicksort possui complexidade da ordem no pior caso, quando a pivotação gera uma partição com elementos e a outra vazia.
Durante o estudo e implementação deste trabalho, alguns trabalhos relacionados foram relevantes e podem ser úteis para os interessados no assunto. Esses trabalhos são suscintamente descritos a seguir.
No livro The Design and Analysis of Computer Algorithms [1] é apresentado um algoritmo para encontrar o -ésimo elemento, cuja complexidade é linear. A conjugação desse algoritmo, com o algoritmo Quicksort Parcial implementado nesse trabalho seria a melhor opção encontrada para o problema da ordenação parcial. A implementação desse algoritmo para encontrar o pivô teria complexidade linear. O k-ésimo menor elemento seria escolhido para ser o pivô do algoritmo de ordenação parcial Quicksort Parcial, o que teria complexidade
. Portanto esse algoritmo conjugado com a solução apresentada teria complexidade
.
Existe uma função em C++ que realiza ordenação parcial. Essa função, denominada partial_sort é baseada historicamente no Heapsort, sendo que sempre ordena os primeiros elementos de um conjunto com elementos em ordem de complexidade 
. Mais referências sobre essa função podem ser obtidas em [7].
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.48)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 trabalho1
The translation was initiated by Adriano Cesar Machado Pereira on 2003-05-19
