UNIVERSIDADE FEDERAL DE MINAS GERAIS

DEPARTAMENTO DE CIÊNCIA DA COMPUTAÇÃO

MESTRADO EM CIÊNCIA DA COMPUTAÇÃO

Primeiro Trabalho Prático da

Disciplina Projeto e Análise de Algoritmos

(www.dcc.ufmg.br/~maxm/disciplinas/paa/tp/tp1/index.html)

Max do Val Machado

e-mail: maxm@dcc.ufmg.brMax

home page: www.dcc.ufmg.br/~maxm

Belo Horizonte, 16 de maio de 2003.

(1) Avaliar as somas (0,5 + 0,5 + 0,5 pontos):

1.

Solução utilizando o método de perturbação descrito em [01, 02] por Knuth

Sabe-se que

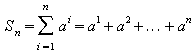(1)

Multiplicando os dois lados por a, tem-se:

(2)

Subtraindo (1) de (2):

Portanto:

e

2.

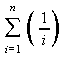
Segundo Cormen em [03] quando uma soma pode ser expressada por 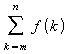e f(k) é uma função monotonicamente decrescente, pode-se aproximar a soma pelo valor das integrais:

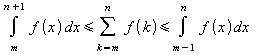
A figura abaixo ilustra a relação ora descrita:

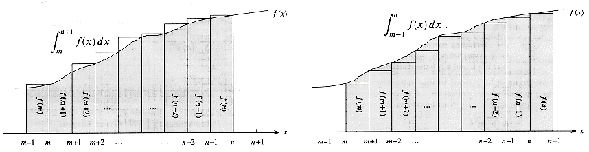
Logo,

=> =>

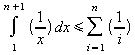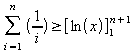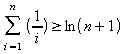
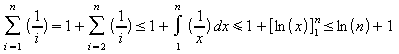
Portanto,

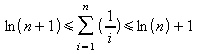
3.

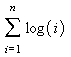
Observa-se:

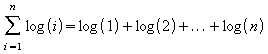
Sabe-se da literatura [01, 04, 03, 05] que:

Logo,

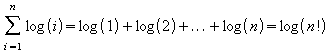
Utilizando a fórmula aproximada para o fatorial [03]:

Tem-se:

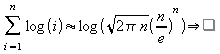
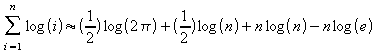
Portanto:

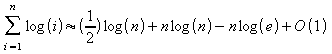
(2) Apresente a complexidade de tempo para os procedimentos abaixo: (0,5 + 0.5 + 0.5 + 0.5 pontos)

1.

Pesquisa(n);

if n <= 1

then termine

else begin

obtenha o maior elemento dentre os n elementos;

{ de alguma forma isto permite descartar 2/5 dos }

{ elementos e fazer uma chamada recursiva no resto }

Pesquisa(3n/5);

end;

a) Unidade de medida: número de comparações para obter o maior elemento.

b) Importante: Na presente questão considerou-se que são necessárias n comparações para se obter o maior elemento entre os n elementos do vetor.

c) Equações:

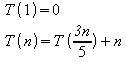
d) Fazendo:

Tem-se:

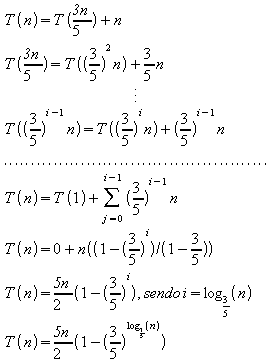
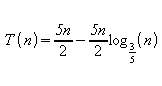
2.

FUNCTION Fib(n: integer): integer;

BEGIN

IF n = 0

THEN Fib := 0

ELSE IF n = 1

THEN Fib := 1

ELSE Fib := Fib(n-1) + Fib(n-2)

END;

a) Unidade de medida: número de atribuições

b) Equações:

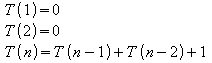
c) Fazendo:

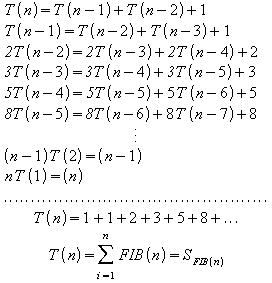
Em [05], Ross e Wright mostram que equações de recorrência do tipo S_n = a S_n-1 + b S_{n -2} (onde a e b são constantes) podem ser resolvidas utilizando as equações características das equações de recorrência. Se a = 0, os autores provam que S_2n+1 = bⁿ S₁. De forma similar, eles provam que se b = 0 então S_n = aⁿ S₀. No entanto, se a e b forem diferentes de zero, como no caso da seqüência de Fibonacci, os autores afirmam ter observado que algumas soluções se apresentam na forma S_n = c rⁿ (onde c é uma constante). Sendo isso verdadeiro, tem-se:

rⁿ = a r ^{n -1} + b r ^{n - 2}

Dividindo a equação acima por r ^{n - 2} obtêm-se r ² = a r + b ou r ² - a r - b = 0. Em outrás palavras, se S_n = c rⁿ para todo n, então, r deve ser a solução da equação de segundo grau x² - a x - b = 0 e essa é conhecida como equação característica das equações de recorrência. É importante destacar que [05] apresenta um teorema em que se a equação característica de S_n = a S_n-1 + b S_{n -2} possuir duas raízes distintas então S_n = c₁ r₁ⁿ + c₂ r₂ⁿ . Se a mesma possuir duas raízes iguais então S_n = c₁ rⁿ + c₂ rⁿ.

Dessa forma, escreve-se S(n) para S_FIB(n) e tem-se S₀ = S₁ = 1 e S_n = S_{n -1} + S_n-2 para n >= 2. Assim, observa-se que a = b = 1 e x² - x - 1 = 0. Pela equação do segundo grau verifica-se as seguintes raízes

e

Logo,

Os valores de c₁ e c₂ podem ser obtidos através de um sistema com n = 0 e n = 1:

1 = c₁ + c₂ e 1 = c₁ r₁ + c₂ r₂

Substituindo c₂ por 1 - c₁ na segunda equação tem-se:

Sendoe , tem-se:

e

Logo,

Portanto:

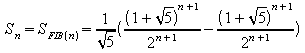
3.

PROCEDURE Sort1 ( VAR A: ARRAY[1..n] OF integer;

i, j: integer );

{ n uma potencia de 2 }

BEGIN

IF i < j

THEN BEGIN

m := (i + j - 1)/2;

Sort1(A,i,m);

Sort1(A,m+1,j);

Merge(A,i,m,j);

{ Merge intercala A[i..m] e A[m+1..j] em A[i..j] }

END;

END;

a) Unidade de medida: número de comparações

b) Equações:

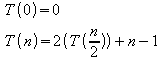
c) Fazendo:

Tem-se:

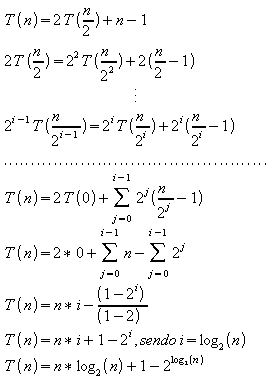
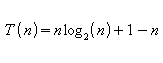
4. PROCEDURE Sort2 ( VAR A: ARRAY[1..n] OF integer;

i, j: integer );

{ n uma potencia de 3 }

BEGIN

IF i < j

THEN BEGIN

m := ( (j - i) + 1 )/3;

Sort2(A,i,i+m-1);

Sort2(A,i+m,i+ 2m -1);

Sort2(A,i+2m,j);

Merge(A,i,i+m,i+2m, j);

{ Merge intercala A[i..(i+m-1)], A[(i+m)..(i+2m-1) e

A[i+2m..j] em A[i..j] a um custo ( (5n/3) -2 ) }

END;

END;

a) Unidade de medida: número de comparações

b) Equações:

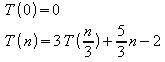
c) Fazendo:

Tem-se:

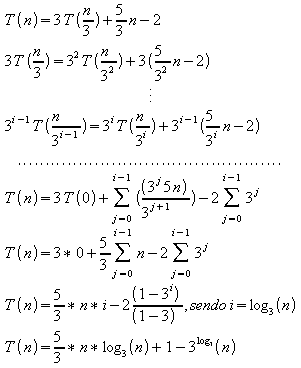
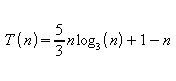
(3) Limite inferior: (1,5 pontos)

Obtenha o limite inferior para ordenar um conjunto de números inteiros usando comparação entre chaves.

Em [03], Knuth afirma que o número mínimo de comparações entre chaves para se ordenar n elementos obviamente é zero. Tal valor pode ser observado nos métodos radix em que não se efetuam comparações entre chaves. No entanto, sabe-se que uma parcela extremamente significativa de métodos de ordenação são baseados na comparação entre chaves, logo verifica-se a importância do limite inferior solicitado na presente questão. Antes de detalhar a solução encontrada é importante destacar que o tempo de execução de um algoritmo de ordenação não é influenciado exclusivamente pelo número de comparações entre chaves que o mesmo realiza. Ele também é influenciado por outros fatores, como por exemplo, a movimentação de dados e as operações internas realizadas.

Na solução encontrada para o limite mínimo de comparações na ordenação de um vetor contendo n elementos, observou-se a criação de uma árvore binária de comparações. Essa é composta por nodos terminais, nodos intermediários e galhos. Nos primeiros, observa-se a existência de uma permutação sem repetição entre todas as combinações possíveis dos índices do vetor de elementos. Logo, conclui-se a existência de n! nodos terminais. Nos nodos intermediários, nota-se a presença de dois índices cujo elemento existente na posição indicada por cada um deles será comparado com o elemento apontado pelo outro índice. Nos galhos, verifica-se uma diferença relativa a localização dos mesmos no nodo. Os da direita indicam que a comparação realizada no nodo pai teve o elemento apontado pelo primeiro índice como sendo o maior dos dois; enquanto os localizados esquerda indicam o contrário. Destaca-se que [03] mostra a viabilidade da solução quando os dois índices existentes em um nodo intermediário apontarem para elementos de mesmo valor. A figura 01 mostra a árvore de comparação para um vetor de três elementos.

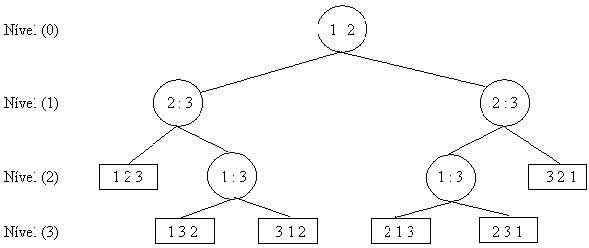
Figura (01): Árvore de comparações para ordenação de três elementos

Outra questão importante é que a solução não realiza comparações desnecessárias, ou seja, comparações que podem ser obtidas de maneira implícita. Isso é feito de acordo com o objetivo proposto de obter a ordem dos n elementos com o menor número de comparações possível. Um exemplo desta economia pode ser observado na figura 01 a partir do nodo raiz, quando se verifica que o elemento apontado pelo índice 1 é o menor. Neste caso, o próximo nodo a ser verificado é o filho à esquerda que compara os elementos apontados pelos índices 2 e 3. Caso o terceiro índice seja maior, o algoritmo aplicado identifica a ordem dos elementos sem comparar diretamente os elementos apontados pelos índices 1 e 3. Tal comparação é desnecessária porque se o elemento apontado pelo índice 1 é menor que o apontado pelo índice 2 e esse é menor que o apontado pelo índice 3, conclui-se trivialmente que o elemento apontado por 1 é menor que o apontado por 3.

Analisando o melhor pior caso (em termos de número de comparações) para a ordenação de n elementos, ou seja, obtendo o limite inferior:

Seja: S(n) o número mínimo de comparações para se ordenar os n elementos.

Se: Todos os nodos intermediários da árvore binária de comparação encontram-se abaixo do último nível (K), é óbvio que número máximo de nodos terminais é 2^K.

Logo: Fazendo K = S(n)

Sendo: S(n) um inteiro, pode-se reescrever a fórmula acima para se obter o limite mínimo

Pela aproximação de Stirling observa-se:

Portanto:

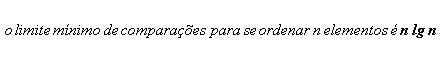
(4) Algoritmos de ordenação parcial: estudos comparativos (1,5 + 1,5 + 1,5 + 0,5 pontos)

O problema da ordenação parcial ocorre quando se deseja obter os k primeiros elementos de um arranjo contendo n elementos, em uma ordem ascendente ou descendente. Quando k = 1 o problema se reduz a encontrar o mínimo (ou o máximo) de um conjunto de elementos. Quando k = n caímos no problema clássico de ordenação.

O problema da ordenação parcial ocorre em muitas situações práticas (Barbosa, 2003). Por exemplo, para facilitar a busca de informação na Web existem as máquinas de busca, que são sistemas para recuperação de informação na Web (Baeza-Yates e Ribeiro-Neto, 1999; Witten, Mofat e Bell, 1999) É comum uma consulta na Web retornar centenas de milhares de documentos relacionados com a consulta. Entretanto, o usuário está interessado apenas nos k documentos mais relevantes, onde k, em geral, é menor do que 200 documentos (na realidade o usuário consulta apenas os 10 primeiros documentos mostrados na primeira página de resposta na maioria das vezes). Consequentemente, a comunidade de recuperação de informação necessita de algoritmos eficientes de ordenação parcial.

O objetivo deste trabalho é realizar um estudo comparativo dos principais algoritmos de ordenação interna que possam ser adaptados para realizar eficientemente ordenação parcial. Assim, considere os seguintes algoritmos de ordenação interna: Inserção, Shellsort, Heapsort, Quicksort (Ziviani, 1993).

1. Determine experimentalmente o número esperado de (i) comparações e (ii) movimentos-de-registro para cada um dos métodos de ordenação indicados acima.

2. Utilize arquivos de diferentes tamanhos com chaves geradas randomicamente. Use o programa Permut.c apresentado abaixo para obter uma permutação randômica de n valores. Repita cada experimento algumas vezes e obtenha a média para cada medida de complexidade. Dê a sua interpretação dos dados obtidos, comparando-os com resultados analíticos.

3. Uma opção alternativa é considerar os mesmos algoritmos propostos e determinar experimentalmente o tempo de execução de cada um dos métodos de ordenação indicados acima.

Use o programa Permut.c para gerar arquivos de tamanhos 1.000, 10.000, 100.000 e 1.000.000 de registros. Para cada tamanho de arquivo dê a sua interpretação dos dados obtidos.

Apresente resultados analíticos para os algoritmos estudados. Considere diferentes valores de k, tais como k = 1, k = 2, k << n, e k = n, onde o caso k << n é o mais interessante.

4. Procure trabalhos relacionados na literatura (se houver) que tratem do assunto e descreva sucintamente esses trabalhos.

RESPOSTA:

Algoritmos Utilizados:

(A) Inserção,

(B) Seleção,

(C) Shellsort,

(D) Heapsort,

(E) Quicksort e

(F) Parcialsort.

Alterações Realizadas nos Algoritmos Originais:

(A) Inserção: O algoritmo original teve seu código duplicado. Na primeira parte, observa-se o algoritmo original da inserção, porém para os primeiros k elementos. Na segunda parte, inserida para a ordenação parcial, verifica-se um anel percorrendo os n - k elementos restantes. Caso o algoritmo encontre algum elemento menor que o maior elemento do conjunto ordenado, então, este elemento é inserido na posição k (que corresponde ao maior elemento do conjunto). Em seguida, um anel similar ao interno do algoritmo original é realizado para re-ordenar o conjunto devido a inserção do novo valor.

(B) Seleção: Neste algoritmo, alterou-se o anel externo do algoritmo original para percorrer apenas os k primeiros elementos e não mais os n-1 primeiros elementos do vetor.

(C) Shellsort: Inicialmente o algoritmo original teve seu código alterado para ordenar apenas os k primeiros elementos em vez de ordenar o vetor completo. Dessa forma, foi inserido um trecho de código complementar para tratar os n - k elementos restantes, garantindo assim, que os k primeiros elementos são os k menores e que esses encontram-se ordenados. Durante a execução deste trecho complementar, quando o algoritmo encontra algum elemento menor que o maior elemento do sub-conjunto ordenado, então, aquele elemento é inserido na posição k (que corresponde ao maior elemento do conjunto). Neste ponto, o algoritmo ainda deve percorrer os k elementos e verificar a posição correta do elemento recém inserido. Destaca-se que este código complementar foi exatamente igual ao complemento inserido no algoritmo da Inserção.

(D) Heapsort: Na alteração realizada, o heap passa a ter apenas k elementos e não mais n. Após a construção do heap (contendo os k primeiros elementos), o algoritmo percorre os n - k elementos restantes. Caso encontre algum elemento menor que o maior elemento do heap, ambos são trocados e o heap é refeito. Quando o algoritmo percorre todos os elementos, ou seja, tem-se certeza que os k menores encontram-se no heap, a fase de manutenção é realizada, ordenando assim, os k menores elementos.

(E) Quicksort: O algoritmo original particiona o vetor em dois grupos distintos de elementos: o dos menores e o dos maiores que a chave particionadora. Em seguida, o algoritmo original efetua uma chamada recursiva para ordenar cada um dos grupos. O processo se repete até que o vetor esteja totalmente ordenado. Na versão para ordenação parcial, a única alteração faz com que o algoritmo só efetue a chamada recursiva para ordenar os elementos maiores que a chave particionadora se e somente se o menor índice do vetor a ser formado for menor ou igual a k.

(F) Parcialsort: Este algoritmo foi desenvolvido a título de comparação entre os algoritmos do Quicksort e do Heapsort. Dessa forma, o Parcialsort constrói um heap com os k primeiros elementos do vetor. Depois, o algoritmo em questão percorre os n - k elementos restantes. Caso encontre algum elemento menor que o maior elemento do heap, ambos são trocados e o heap é refeito. Quando o algoritmo percorre todos os elementos, o mesmo invoca o quicksort para ordenar os k menores elementos do heap.

Número esperado de: (i) comparações e (ii) movimentos de registros

(A) Inserção: Conforme descrito acima e verificado no código em anexo, a análise do algoritmo em questão será dividida em duas partes. Destaca-se que o melhor caso deste algoritmo ocorre quando o vetor estiver ordenado em ordem crescente e o pior caso ocorre quando o vetor estiver ordenado em ordem decrescente.

1. Comparações:

   1. Melhor Caso:

O algoritmo executa o anel externo da primeira parte k - 1 vezes e para cada uma dessas o mesmo efetua uma comparação que nunca o faz entrar no anel interno. Dessa forma, o número de comparações da primeira parte é:

Na segunda parte, o algoritmo é verifica os n - k elementos restantes do conjunto e verifica que todos são menores que o k-ésimo maior elemento do conjunto já ordenado. Logo, o número de comparações é:

Somando os resultados verifica-se:

2. Pior Caso:

Observando o anel interno da primeira parte verifica-se que o mesmo é executado i vezes, logo (2 + 3 + ... + k). [07] mostra que o valor deste somatório é:

Para a segunda parte verifica-se que o anel interno efetua (k + 1) comparações para cada um dos (n -k) elementos restantes. Logo, observa-se:

Somando os resultados verifica-se:

3. Caso Médio:

Considerando que a probabilidade de um elemento ser maior que seu sucessor é ½, tem-se na primeira parte:

Na segunda parte, verifica-se que metade das vezes tem-se (n - k) e na outra (n - k) (k + 1) comparações. Logo:

Somando os resultados verifica-se:

2. movimentos-de-registro: Neste caso, verifica-se que o número de movimentações é igual a soma dos movimentos realizados na primeira parte, mais os da segunda e mais um movimento realizado entre as duas partes. Destaca-se ainda que na segunda parte verifica-se que para cada interação do anel interno uma movimentação de registro é executado, enquanto para o anel externo 7 movimentações são executadas.

1. Melhor Caso:

O algoritmo executa o anel externo da primeira parte k - 1 vezes e para cada uma delas o mesmo efetua 3 movimentações de registro, logo:

Na segunda parte, verifica-se que o algoritmo não executa nenhuma movimentação de registro uma vez que todos os elementos são menores que o elemento comparado:

Somando os resultados verifica-se (lembrando do movimento realizado entre as duas partes):

2. Pior Caso:

Observando o anel interno da primeira parte verifica-se que o mesmo é executado i vezes, logo são realizadas (4 + 5 + ... + k + 2) movimentações. [07] mostra que o valor deste somatório é:

Para a segunda parte, verifica-se que o anel externo é realizado uma vez para da um dos (n - k) elementos restantes, e, para cada um desses o anel interno é executado (k - 1) vez. Conforme mencionado o anel externo efetua uma movimentação e o interno efetua 7 movimentações. Logo, observa-se:

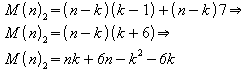
Somando os resultados verifica-se (lembrando do movimento realizado entre as duas partes):

3. Caso Médio:

Considerando que a probabilidade de um elemento ser maior que seu sucessor é ½, tem-se na primeira parte que o número de movimentos é ½ ( 5 + 6 + ... + n + 3). [07] mostra que o valor deste somatório é:

Na segunda parte, verifica-se que metade das vezes tem-se 7(n - k) movimentações e outra metade tem-se (n - k) (k - 1) movimentações.

Somando os resultados verifica-se (lembrando do movimento realizado entre as duas partes):

(B) Seleção: Conforme descrito acima e verificado no código em anexo, alterou-se o anel externo do algoritmo original para percorrer apenas os k primeiros elementos e não mais os n-1 primeiros elementos do vetor. Outra consideração a respeito deste algoritmo é que se o vetor de entrada já estiver ordenado, ele efetua o mesmo número de comparações e de movimentações de registros.

1. Comparações:

Verifica-se que em cada interação do anel externo n - i interações do anel interno são executadas, onde i é o apontador que percorre o vetor. Sabendo-se que a cada interação do anel interno uma comparação é realizada, tem-se:

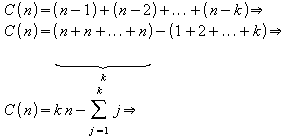
2. movimentos-de-registro:

Analisando o algoritmo observa-se que o mesmo sempre efetua 3 movimentos de registros por interação do anel externo e sabendo que esse é executado três vezes, tem-se:

(C) Shellsort:

Em [07], Ziviane afirma que: '' (...) a razão pela qual o Shellsort é eficiente não é conhecida, porque ninguém ainda foi capaz de analisar o algoritmo. A sua análise contém alguns problemas matemáticos muito difíceis, a começar pela própria sequência de incrementos: o pouco que se sabe é que cada incremento não deve ser múltiplo do anterior. Para a sequência de incrementos utilizada no programa 3.5 existem duas conjecturas para o número de comparações (...)''. Neste ponto é fundamental afirmar que o programa de [07] equivale a primeira parte do algoritmo Shellsort para ordenação parcial desenvolvida no presente trabalho e que as duas conjecturas mencionadas para o número de comparações, são:

e

Sobre a analise do Shellsort, em [06], Knuth afirma: '' (...) This leads to some fascinating mathematical problems, not yet completely resolved; nobody has been able to determine the best sequence of increments for large N. Yet a good many interesting facts are known about the behavior of shellsort (...)''.

Como o algoritmo Shellsort para ordenação parcial desenvolvido apresenta duas partes e a primeira delas equivale ao algoritmo original do Shellsort, porém para k elementos e não para n. O presente trabalho considera que o número de comparações da primeira parte é igual a primeira conjectura. Para a segunda parte, conforme mencionado anteriormente, a mesma é igual a segunda parte do algoritmo da Inserção para ordenação parcial aqui desenvolvida. Logo, o melhor caso, o pior caso e o caso médio ocorrem conforme o descrito no algoritmo da Inserção. Dessa forma, tem-se as fórmulas abaixo:

1. comparações:

1. Melhor Caso:

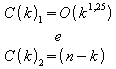
2. Pior Caso:

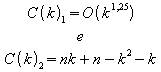
3. Caso Médio:

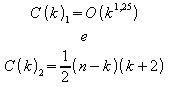
(D) Heapsort:

Conforme mencionado anteriormente e verificado no código em anexo, o algoritmo do heapsort para ordenação parcial forma um heap com os k primeiros elementos. Em seguida, o mesmo compara cada um dos n - k elementos restantes com a raiz do heap. Se o elemento comparado for menor que a raiz (maior elemento do heap), então ambos tem sua posição alterada, ou seja, o elemento que estava no heap sai e o outro entra. No passo seguinte, após percorrer os n - k elementos restantes, o algoritmo efetua o processo de ordenação do heap contendo os k menores elementos.

Com vista a simplificação da análise, o valor de k a ser considerado será um número par. Isso faz com que as condições do heap possam ser apresentadas sem nenhuma exceção gerada devido a não existência do termo . Tal consideração pode ser verificada abaixo nas divisões k / 2 ao invés das divisões inteiras k div 2. Destaca-se que se k fosse impar os resultados de analise apresentados teriam um erro de meia unidade por divisão. Assim, o número de comparações no melhor caso será considerando como sendo igual a k e não a 2 *(k div 2).

O melhor caso do Heapsort para ordenação parcial é verificado quando os k menores elementos encontram-se no heap e dispostos inicialmente de forma que as condições , para i = 1, k div 2 (conforme mencionado na técnica para a simplificação da análise). Uma permutação que satisfaz tais condições ocorre quando os k menores elementos forem os primeiros do heap e os mesmos encontrarem-se ordenados em ordem decrescente. Neste caso, a árvore derivada já forma um heap, não sendo necessária nenhuma movimentação de registro. Apenas serão efetuadas 2 * (k / 2) comparações (duas para cada subárvores testada), para se certificar de que a árvore é um heap. No passo seguinte, os n - k elementos serão descartados com apenas n - k - 1 comparações porque todos eles são maiores que a raiz do heap.

Pelo lado contrário, o pior caso ocorre quando: os k maiores elementos se encontrarem nas k primeiras posições e ordenados em ordem crescente; e os n - k elementos restantes devem estar ordenados de forma decrescente. Nesta situação, para o processo de formação do heap observam-se movimentações de registros proveinientes das comparações realizadas nas k / 2 subárvores. Como a condição de heap nunca encontra-se presente no vetor inicial, cada movimentação de registro em um nível da árvore irá afetar todas as subárvores daquele nível. Destaca-se que isto ocorre no pior caso porque as chaves rebaixadas em cada subárvore serão sempre as menores, logo, elas deverão se localizar nas folhas. No segundo passo, quando se compara cada um dos n – k elementos com a raiz do heap, sempre a raiz é maior. Logo, ambos devem ser trocados e a nova raiz desfaz a condição de heap (devido a configuração original, a nova raiz é menor que qualquer elemento do heap). Neste ponto, observa-se a necessidade de trocas de registros proveinientes das comparações realizadas nas k / 2 subárvores, além disso, uma troca em um nível qualquer faz com que novas trocas ocorram em todos os níveis inferiores da subárvore até que o elemento chegue ao nível das folhas. Assim, sempre, seja no primeiro ou no segundo passo, ter-se-á as k comparações seguidas de k / 2 trocas, acrescidas daquelas comparações e trocas referentes ao escorregamento das chaves menores até o nível das folhas.

Desta forma, a análise aqui apresentada para o algoritmo Heapsort para ordenação parcial será composto de três fases: a formação do heap inicial, a definição dos k menores elementos e a sua manutenção.

Formação do Heap

Segundo [08], para se calcular a quantidade extra de comparações e trocas, pode-se usar a técnica da indução, calculando quantas serão efetuadas a partir de cada nível da árvore, iniciando pela raiz (nível 1) e obtendo, a seguir, a expressão que generaliza para qualquer nível. No caso da subárvore da raiz, tem-se uma uma troca para que ela, isoladamente, forme um heap, seguida de trocas correspondentes ao escorregamento da chave rebaixada até o nível das folhas. No nível 2, além das duas trocas correspondentes às duas subárvores deste nível, tem-se trocas devidas ao escorregamento até o nível das folhas. Isso ocorre de maneira sucessiva até o penúltimo nível em que só ocorrerão trocas referentes à transformação das subárvores em heaps (no último nível não existem propagações). A tabela (01) mostra a quantidade de trocas efetuadas em cada nível:

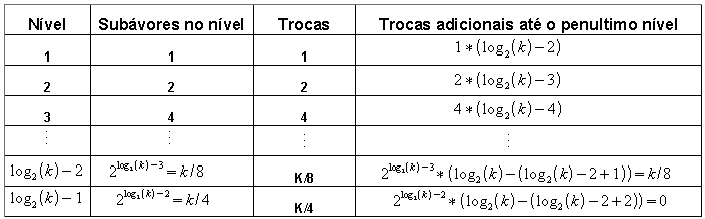
Tabela (01): Quantidade de trocas efetuadas em cada nível

A soma dos valores da terceira coluna corresponde ao total de trocas efetuadas para transformar cada uma das k / 2 subárvores em heaps, sem contar o escorregamento. Segundo [08], k /4 + k / 8 + ... + 2 + 1 = k / 2. O total de trocas referentes ao escorregamento é a soma dos valores da quarta coluna. Para se obter este total, usou-se o seguinte artifício: considerou-se o valor das parcelas a serem somadas como sendo a soma de potências inteiras de 2, conforme mostrado na tabela (02).

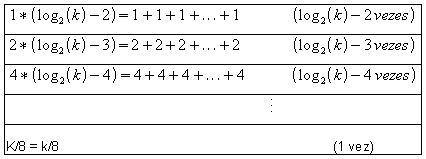
Tabela (02): Artifício utilizado para calcular as parcelas

Tomando agora as potências de 2 e, ao invés de somá-las na horizontal, soma-se coluna por coluna, conforme a tabela (03).

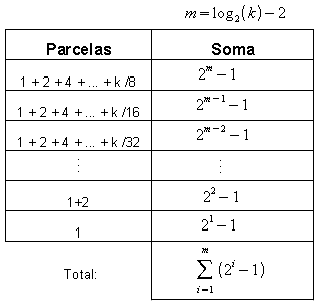
Tabela (03): Soma das parcelas por coluna

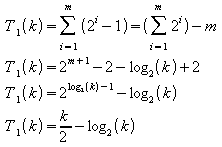
Acrescentando as k / 2 trocas correspondentes à soma da terceira coluna da tabela (01), tem-se que o total de movimentações para a formação do heap, no pior caso para o método, é:

No entanto, sabe-se que cada troca implica em três movimentações de registros e duas comparações, logo:

e

A Tabela (04) resume as quantidades mínimas e máximas de movimentações e comparações efetuadas na fase de formação:

Tabela (04): Resumo das quantidades de operações

Definição dos k menores elementos

Para cada um dos n – k elementos restantes temos duas situações: elemento maior ou igual a raiz ou elemento menor que a raiz. No primeiro caso, o elemento é descartado sem nenhuma troca ou comparação extra. No segundo caso, o elemento deve ser trocado com a raiz e devem haver trocas internas no heap para que a condição de heap permaneça. Neste caso, a melhor hipótesee ocorre quando o elemento é menor que a raiz e maior que os dois filhos daquela. Logo, foram necessárias (a partir do ponto que a nova raiz já se encontre na posição de raiz) apenas duas comparações e nenhuma troca para que as condições de heap fossem garantidas após a inserção da nova raiz. Ainda para o segundo caso, a pior hipótesee (também considerando que a a nova raiz já se encontre na posição de raiz) ocorre quando a nova raiz é menor que pelo menos um elemento do último nível. Neste caso, o número de trocas obedecerá a primeira linha da tabela (01), ou seja, serão efetuadas trocas.

Dessa forma, no melhor caso do algoritmo existem apenas n – k comparações para se verificar que os k menores elementos encontram-se na raiz. Na melhor hipótese do pior caso tem-se as n – k comparações para se verificar que o elemento da vez é menor que a raiz e mais 2 (n – k) comparações para se verificar que o mesmo é maior que seus filhos. Logo, o número de trocas é igual a n – k e o número de movimentações é igual 3(n – k). Na pior hipótesee do pior caso, existem as n – k comparações para se determinar que o elemento é menor que a raiz (n – k trocas e 3n – 3k movimentos), mais as trocas para que o elemento escorregue até o nível das folhas (comparações e movimentos).

No caso médio, tem-se que metade das vezes o elemento é maior que a raiz e na outra metade é maior. Isso porque a probabilidade de um caso ou outro é de ½. No segundo caso, metade (da metade) das vezes o elemento é maior que os filhos da raiz e na outra metade o mesmo é menor que pelo menos uma das folhas. Neste caso, a probabilidade também é igual a ½. A tabela abaixo mostra os valores para os três casos:

Tabela (05): Resumo dos casos para a definição dos k menores elementos

Manutenção do Heap

Na fase de manutenção, partindo do heap formado anteriormente, sempre que a chave que ocupava a raiz da árvore for colocada, por troca, na parte final do vetor, será necessário refazer o heap. Nesta operação, a chave que passou a ocupar a raiz deverá escorregar de volta em direção às folhas, até encontrar a sua posição correta [08].

Dois casos podem ocorrer nessa operação. Se a chave descer de volta pelo mesmo lado da árvore de onde proveio, então ela retornará ao nível das folhas. Caso, no entanto, desça pelo outro lado, ela poderá parar em qualquer nível, desde o segundo até o último. O lado da árvore pelo qual as chaves descerão será aquele cuja subárvore da raiz contenha o maior valor. Como as chaves que estão em um mesmo nível não possuem obrigatoriamente nenhuma relação de ordem entre si, pode-se supor que a probabilidade de descerem por um lado ou por outro é a mesma e igual a ½. Assim, é válido afirmar que aproximadamente metade das chaves descerão pelo mesmo lado de onde provêm, e consequentemente, retornarão ao nível das folhas, enquanto a outra metade que descerá pelo lado oposto, estacionando em um nível intermediário da árvore. Em outrás palavras, metade das chaves descerá à altura instantânea h da árvore, e as restantes à metade (em média) de h, ou seja:

Isto é, tudo se passa como se ¾ das chaves descessem à altura instantânea da árvore a cada interação. Neste ponto, o presente trabalho irá calcular quantas trocas seriam necessárias caso todas as chaves descessem até o nível das folhas e, depois, tomando ¾ do valor obtido será determinado a quantidade média de trocas efetivamente executadas.

Para facilitar a obtenção da função que exprime o número de trocas efetuadas, o processo de manutenção do heap será revisto de trás para diante. Neste caso, as trocas serão contadas a partir da última interação, quando a árvore possui apenas o elemento da raiz. E depois, retornando até o ponto que corresponde ao início do processo, quando a árvore possui n chaves. Desta forma, quando a altura h da árvore for igual a 1, ter-se-á uma chave que não descerá nível algum Destaca-se que para h = 2, são 2 chaves descendo um nível, enquanto para h = 3, tem-se 4 chaves descendo dois níveis. E assim até h = m (altura inicial), quando então, todas as chaves deste nível descerão m – 1 níveis.

Como cada vez que uma chave desce um nível observa-se uma troca, o total de trocas será a soma das trocas realizadas para que todas as chaves voltem ao nível das folhas. A tabela 06 mostra o total de trocas correspondente a cada altura da árvore (supondo que a árvore inicial seja completa, ou seja, que todas as folhas estejam no mesmo nível):

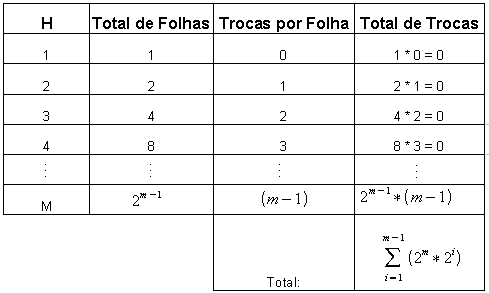
Tabela(06): Total de trocas correspondente a cada altura da árvore

Usando um artifício semelhante ao utilizado para calcular as trocas adicionais para a formação do heap, tem-se:

Tabela (07): Artifício para calcular o número de trocas adicionais

Somando as parcelas tem-se:

Tabela (08): Soma das parcelas na fase de manutenção

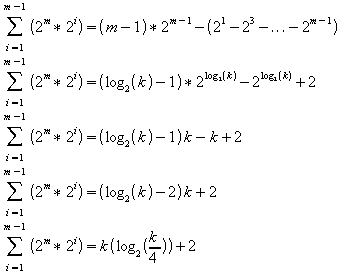
Tomando, finalmente, a fração de ¾ deste valor, que corresponde ao número equivalente de chaves que descem da raiz até o nível das folhas. Esse novo valor corresponde à quantidade média de trocas efetuadas durante a fase de manutenção do heap. É importante recordar que ao resultado também deve-se acrescentar o valor k -1, correspondente às trocas efetuadas para colocar as chaves da raiz no heap em suas posições corretas.

e

As comparações sempre corresponderão ao dobro das trocas, sem a parcela k – 1 acrescida no final, pois as trocas correspondentes a esta parcela não são procedidas de comparações. Já as movimentações de registros correspondem a 3 vezes o número de trocas

e

e

Ao longo desta análise foi suposto que a árvore inicial tivesse todas as suas folhas no mesmo nível, isto é, que a árvore possuísse no nível m, chaves, o que nem sempre ocorre. Na realidade, isto só é verdade quando , para i inteiro. Qualquer outro valor de k fará com que as folhas se distribuam em dois níveis consecutivos, sendo no nível m -1 e no nível m. Este fato faz com que o total de trocas efetivamente executadas seja menor do que o valor estimando. Por outro lado, fazendo

1. Comparações e movimentos-de-registro:

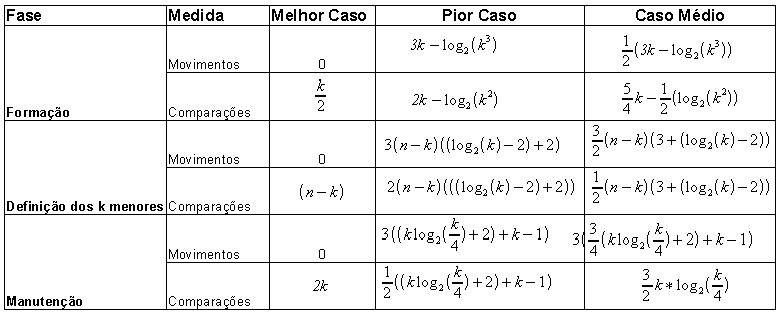
Tabela(09): Comparações e movimentos de registros para: o melhor caso,

o pior caso e o caso médio do Heapsort Parcial

(E) Quicksort:

1. comparações:

   1. Melhor Caso:

Neste caso verifica-se que a situação ideal ocorrerá quando a chave particionadora for o k-ésimo menor elemento do vetor, isso porque com apenas n - 1 comparações o algoritmo terá detectado os k menores elementos. Destaca-se que com apenas esta situação, considerando k << n, o algoritmo do quicksort já apresentará um desempenho extraordinário. No entanto, isso não é suficiente para se afirmar que o caso em discussão trate-se do melhor caso do algoritmo, para isso, os k menores elementos também devem estar ordenados com o menor número de comparações possíveis.

O melhor caso do quicksort para se ordenar k elementos ocorre quando a chave particionadora é tal que o particionamento tem como resultado dois segmentos de mesmo tamanho. Da mesma forma, o particionamento de cada um destes segmentos também deve gerar segmentos de mesmo tamanho. Persistindo a situação ideal ao longo dos demais particionamentos, os segmentos que serão sucessivamente gerados terão comprimentos iguais. O número de comparações de cada um desses segmentos vai requerer, para ser particionado, tantas comparações quantos são seus elementos menos uma unidade. Conforme mostrado em [08], tem-se:

1. Para o primeiro segmento: k - 1 comparações (a partir dos k menores elementos)

2. Para o segundo segmento:(((k - 1)/2)-1)x2 = k - 3 comparações

3. Para o terceiro segmento:(((k - 3)/4)-1)x4 = k - 7 comparações

4. Para o terceiro segmento:(((k – 7)/8)-1)x8 = k - 15 comparações

e assim sucessivamente, enquanto restarem segmentos de mais de um elemento. Esta condição deixará de ocorrer após executados piso do logaritmo de n na base dois passos de particionamento (piso a, sendo a igual ao maior inteiro menor ou igual a).

Logo, o total de comparações a serem executadas para a ordenação dos k primeiros elementos é igual a soma do número de comparações efetuadas em cada passo, ou seja:

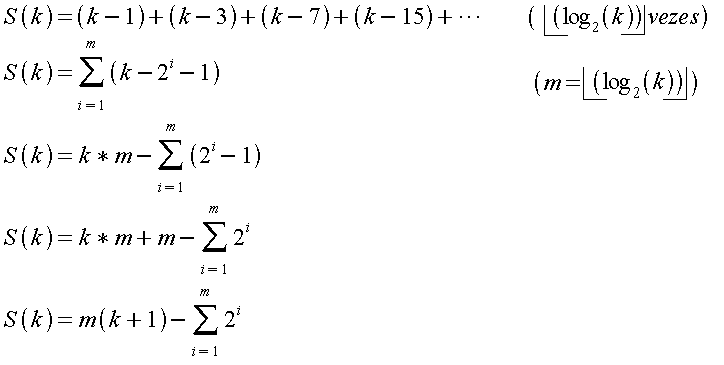
No entanto, o que se deseja não é o melhor caso do quicksort original e sim o do quicksort para ordenação parcial. Conforme mostrado anteriormente, para se determinar os k menores elementos o quicksort efetua no melhor caso n - 1 comparações. Somando os valores tem-se:

2. Pior Caso:

O pior caso, por sua vez, ocorre quando a chave particionadora escolhida é a maior chave de todas. Neste caso, e persistindo a situação em todos os demais particionamentos, o método se torna extremamente lento, com desempenho quadrático. [08] De fato, se a chave escolhida for sempre a maior de todas, os particionamentos produzirão sempre o primeiro segmento vazio e o segundo com n - 1 elementos. Neste ponto, verifica-se uma diferença importante em relação ao pior caso do quicksort original em que esta situação se faz presente seja a chave escolhida a menor ou a maior chave de todas. No quicksort para ordenação parcial se a menor chave for sempre a escolhida, após as k primeiras interações do algoritmo os k primeiros elementos encontrar-se-ão ordenados e o algoritmo descarta as interações com i > k.

Segundo [08], sendo necessários, pois, n - 1 passos, cada um deles exigindo um número de comparações igual ao número de elementos menos um, ou seja:

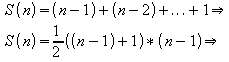
Destaca-se ainda que este caso ocorrerá, por exemplo, se o vetor estiver ordenado e sempre a última chave for escolhida.

(F) Parcialsort:

Conforme mencionado anteriormente e verificado no código em anexo, o algoritmo Parcialsort forma um heap com os k primeiros elementos. Em seguida, o mesmo compara cada um dos n - k elementos restantes com a raiz do heap. Se o elemento comparado for menor que a raiz (maior elemento do heap), então ambos tem sua posição alterada, ou seja, o elemento que estava no heap sai e o outro entra. No passo seguinte, após percorrer os n - k elementos restantes, o algoritmo executa o qucksort original para os k elementos. Logo, o melhor caso, o pior cao e o caso médio ocorrem nas mesmas situações descritas para o heapsort. A diferença entre os valores mostrados na tabela abaixo e os da tabela (09) se diferenciam apenas na terceira fase. No Parcialsort observa-se que a fase de manutenção foi substituída pelo quicksort.

Tabela(10): Comparações para: o melhor caso e pior caso do Parcial sort

Resultados Experimentais:

Para o desenvolvimento da presente questão, optou-se por alterar o código dos algoritmos de ordenação interna fornecidos por Ziviane em [07] para que eles fossem mais propícios para a ordenação parcial de registros. Desta forma, as seguintes etapas foram definidas: (i) alteração dos algoritmos para ordenação parcial; (ii) implementação dos mesmos utilizando a linguagem C; (iii) definição de tamanhos iniciais de vetores (n) a serem ordenados parcialmente; (iv) definição do número de elementos a ser ordenado (k); (v) definição da distribuição inicial dos elementos no vetor; (vi) criação de uma função para definição do intervalo de confiança no caso de simulações cuja a distribuição inicial dos vetores encontrava-se de forma aleatória; (vii) definição dos resultados desejados sobre cada simulação.

1. - As alterações efetuadas foram as descritas anteriormente.

2. - O código encontra-se em anexo.

3. - Os tamanhos iniciais (n) dos vetores utilizados no presente trabalho foram: 1.000, 10.000, 100.000 e 1.000.000

4. - O número de elementos a ser ordenados no vetor foram: 1, 2, 10, 100 e n (onde, n corresponde a todos os elementos do vetor inicial).

5. - Os elementos encontravam se dispostos no vetor de três formas: em ordem crescente, em ordem decrescente e em ordem aleatória.

6. - Para a obtenção de cada resultado no caso das simulações cuja distribuição inicial dos elementos no vetor era aleatória, utilizou-se uma amostra composta por 30 simulações sem a alteração de parâmetros, exceto a semente para a geração de números aleatórios. Trabalhou-se também com um intervalo de confiança de 95% para garantir mais confiabilidade aos resultados obtidos. Na verdade, o resultado de cada simulação foi produzido através da média dos valores para a população da referida amostra.

7. - Sobre cada simulação foram obtidos os números de comparações e de movimentações de registros efetuadas por cada algoritmo, além do tempo de execução do mesmo. Cada simulação teve seus parâmetros alterados conforme descrito nos itens (iii), (iv), (v) e (vi).

A seguir os resultados obtidos são mostrados em quatro grupos: tabelas contendo o tempo de execução e os números de comparações e de movimentos de registros de cada algoritmo com n igual a 1.000.000; tabelas comparando os resultados dos algoritmos simulados utilizando a forma aleatória e com o valor de k sendo variável; tabelas comparando os resultados dos algoritmos simulados utilizando a forma aleatória e com o valor de k sendo variável; tabelas contendo todos os resultados de cada gráfico.

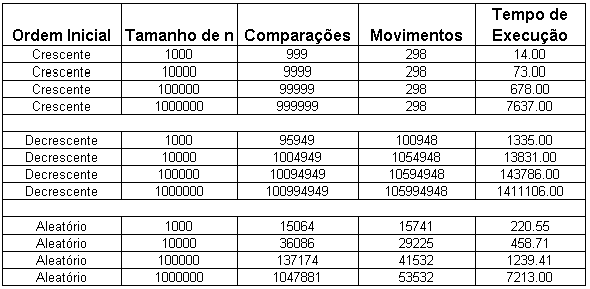
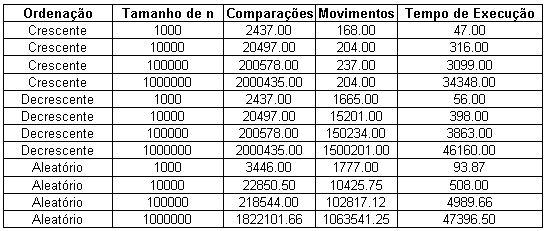
Tabela (11): Algoritmo da Inserção com k = 100

A Tabela (11) mostra alguns resultados de simulação para o algoritmo da Inserção adaptado para ordenação parcial; neste caso variou-se a ordenação inicial do vetor e o tamanho do vetor inicial (n), enquanto o número de elementos a ser ordenados (k) foi mantido constante e igual a 100. Conforme mostrado anteriormente, o melhor caso do algoritmo da Inserção é verificado quando os elementos encontram-se dispostos inicialmente na ordem crescente, enquanto o pior caso é verificado quando os elementos estão inicialmente em ordem crescente.

Para o melhor caso foi mostrado anteriormente que o número de comparações para ordenar o vetor é igual a e o número mínimo de movimentações de registros é igual a . Tais valores são facilmente verificados substituindo os valores de n e de k e comparando-os com as quatro primeiras linhas da tabela (11).

Para o pior caso, os números de comparações e de movimentos de registros foram respectivamente e . Substituindo, por exemplo, k por 100 e n por 1.000.000, observa-se respectivamente: 100.994.949 e 105.994.648.

Para o caso médio, os números de comparações e de movimentos de registros foram respectivamente e . Substituindo, por exemplo, k por 100 e n por 1.000.000, observa-se respectivamente: 50.997.474 e 52.997.473

Ainda com relação a tabela 11 é fácil verificar que o tempo de execução é menor no melhor caso (ordem crescente) e maior no pior caso (ordem decrescente). Destaca-se que o aumento de n implica no aumento do tempo de execução

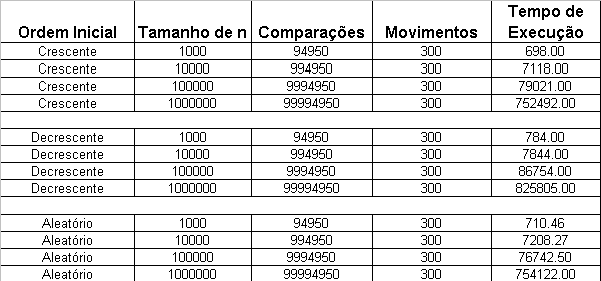
Tabela (12): Algoritmo Seleção

A Tabela (12) mostra alguns resultados de simulação para o algoritmo da Seleção adaptado para ordenação parcial; neste caso variou-se a ordenação inicial do vetor e o tamanho do vetor inicial (n), enquanto o número de elementos a ser ordenados (k) foi mantido constante e igual a 100. Conforme mostrado anteriormente, a ordem de entrada não influência o número de comparações e de movimentos de registros.

Como mostrado anteriormente, o número de comparações para ordenar o vetor é igual a e o número de movimentos de registros é igual a. Tais valores são facilmente verificados substituindo os valores de n e de k e comparando-os os da tabela.

Ainda com relação a tabela 11 verifica-se que o tempo de execução é menor na ordem crescente e maior na ordem decrescente. Sendo o número de comparações e movimentos de registros os mesmos uma explicação para tais resultados seria o fato de tempos distintos para ler elementos em posições distintas. Destaca-se que o aumento de n implica no aumento do tempo de execução.

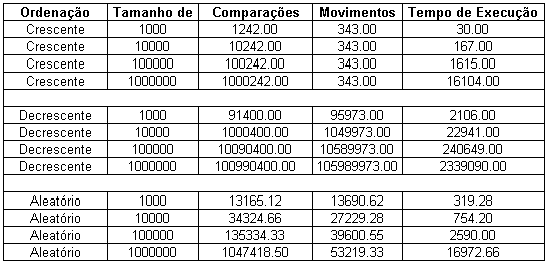
Tabela (13-A): Algoritmo Shellsort

Tabela (13-B): Algoritmo Shellsort

A Tabela (13-A) mostra alguns resultados de simulação para o algoritmo Shellsort adaptado para ordenação parcial; neste caso variou-se a ordenação inicial do vetor e o tamanho do vetor inicial (n), enquanto o número de elementos a ser ordenados (k) foi mantido constante e igual a 100. Conforme mostrado anteriormente, o melhor caso do algoritmo Shellsort é verificado quando os elementos encontram-se dispostos inicialmente na ordem crescente, enquanto o pior caso é verificado quando os elementos estão inicialmente em ordem crescente.

Para o melhor caso foi mostrado anteriormente que o número de comparações para ordenar o vetor é igual a , enquanto para o pior caso e para o caso médio os respectivos valores de tal parâmetro são:e . Tais valores para o melhor e para o pior caso são mostrados na tabela (13-B).

Ainda com relação a tabela 13 é fácil verificar que o tempo de execução é menor no melhor caso (ordem crescente) e maior no pior caso (ordem decrescente). Destaca-se que o aumento de n implica no aumento do tempo de execução

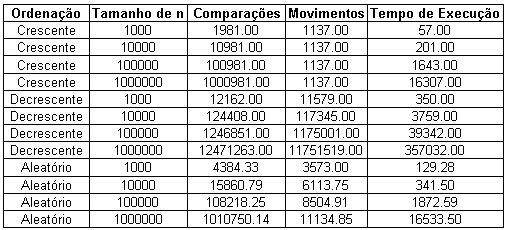
Tabela (14 - A): Algoritmo Heapsort

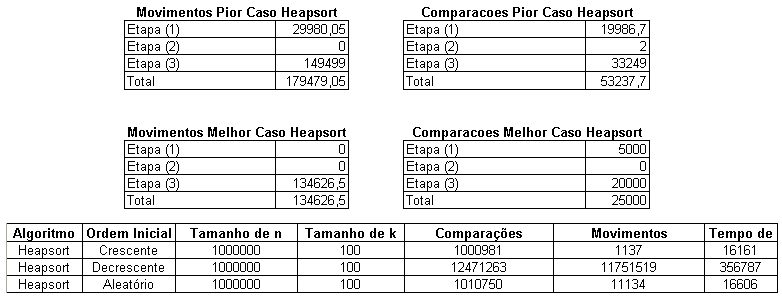
Tabela (14 - B): Algoritmo Heapsort

A Tabela (14) mostra alguns resultados de simulação para o algoritmo Heapsort adaptado para ordenação parcial; neste caso variou-se a ordenação inicial do vetor e o tamanho do vetor inicial (n), enquanto o número de elementos a ser ordenados (k) foi mantido constante e igual a 100. Conforme mostrado anteriormente, o melhor caso do Heapsort para ordenação parcial é verificado quando os k menores elementos encontram-se no heap e dispostos inicialmente de forma que as condições , para i = 1, k / 2. Pelo lado contrário, o pior caso ocorre quando: os k maiores elementos se encontrarem nas k primeiras posições e ordenados em ordem crescente; e os n - k elementos restantes devem estar ordenados de forma decrescente.

Observa-se na tabela (14-B) os números esperados para o melhor e para o pior caso. Ainda na tabela 14-B, verifica-se que os valores do melhor caso encontram-se abaixo dos valores obtidos, assim como, os do pior caso encontram-se acima dos valores obtidos. Neste ponto, é bom recordar que o melhor caso do algoritmo, conforme mostrado anteriormente, não ocorre quando o vetor estiver inicialmente ordenado; e da mesma forma o pior caso não ocorre na situação contrária.

A partir da tabela 14 observa-se que os resultados das simulações com o vetor inicial em ordem crescente foram os melhores e os de ordem decrescente os piores. Esta situação se fez presente apesar do Heapsort original apresentar resultados completamente inversos. Apesar, do maior custo para montar o heap no vetor inicialmente ordenado, esta situação desfavorável é fulminantemente revertida na segunda etapa quando todos os n – k elementos restantes são maiores que a raiz do heap. Desta forma, todos são descartados. Já no vetor inicialmente em ordem decrescente, o custo para se montar o heap é mínimo, porém na segunda etapa todos os elementos pertencente aos n – k restantes são inseridos no heap (e pior, todos são folhas).

Ainda com relação a tabela 14 é fácil verificar que o tempo de execução é menor no melhor caso (ordem crescente) e maior no pior caso (ordem decrescente). Destaca-se que o aumento de n implica no aumento do tempo de execução

Tabela (15-A): Algoritmo Quicksort

Tabela (15-B): Algoritmo Quicksort

A Tabela (15) mostra alguns resultados de simulação para o algoritmo Quicksort adaptado para ordenação parcial; neste caso variou-se a ordenação inicial do vetor e o tamanho do vetor inicial (n), enquanto o número de elementos a ser ordenados (k) foi mantido constante e igual a 100. Conforme mostrado anteriormente, o melhor caso do Quicksort ocorre quando a chave particionadora é tal que o particionamento tem como resultado dois segmentos de mesmo tamanho. Da mesma forma, esta situação deve persistir nas chamadas recursiva e o particionamento de cada segmentos também deve gerar segmentos de mesmo tamanho. O pior caso, por sua vez, ocorre quando a chave particionadora escolhida é a maior chave de todas e a escolha da maior chave persiste nas chamadas recursivas. Observa-se na tabela (15-B) os números esperados para o melhor e para o pior caso. Ainda na tabela 15-B, verifica-se que os valores do melhor caso encontram-se abaixo dos valores obtidos, assim como, os do pior caso encontram-se acima dos valores obtidos.

A partir da tabela 15 observa-se que os resultados das simulações com o vetor inicial em ordem crescente foram iguais em termos de comparações e amplamente divergentes em termos de movimentos de registros. Isso ocorre porque no primeiro caso, os elementos comparados um a um na primeira interação do algoritmo já se encontram em suas respectivas posições e no segundo caso, todos tem suas posições alteradas. Neste ponto, é importante destacar que após a segunda interação a disposição dos elementos é exatamente a mesma e a diferença entre os valores dos números de movimentações de registros foi dada devido a primeira interação.

Outra situação interessante verificada na tabela 15 é que o número de movimentações de registros e comparações efetuadas pelo algoritmo executando sobre um vetor inicialmente em ordem decrescente são maiores que os do algoritmo executando sobre um vetor de ordem inicialmente aleatória. No entanto, no tempo de execução verifica-se o contrário. Isso ocorre porque mesmo efetuando mais comparações e mais movimentação de registro, o algoritmo em ordem decrescente encontra os k menores elementos primeiro. Ainda com relação a tabela 15 (assim como nos algoritmos anteriores), destaca-se que o aumento de n implica no aumento do tempo de execução.

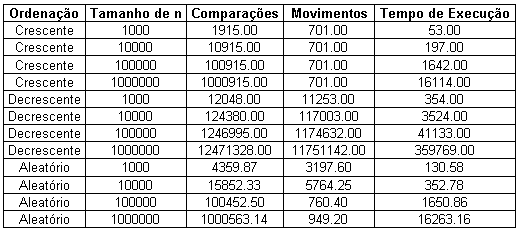
Tabela (16-B): Algoritmo Parcialsort

Tabela (16-B): Algoritmo Parcialsort

A Tabela (16) mostra alguns resultados de simulação para o algoritmo Parcialsort adaptado para ordenação parcial; neste caso variou-se a ordenação inicial do vetor e o tamanho do vetor inicial (n), enquanto o número de elementos a ser ordenados (k) foi mantido constante e igual a 100. Conforme mostrado anteriormente, o melhor caso é exatamente o mesmo do Heapsort para ordenação parcial. Logo, todas as considerações relativas aos resultados obtidos naquele são aplicadas neste algoritmo.

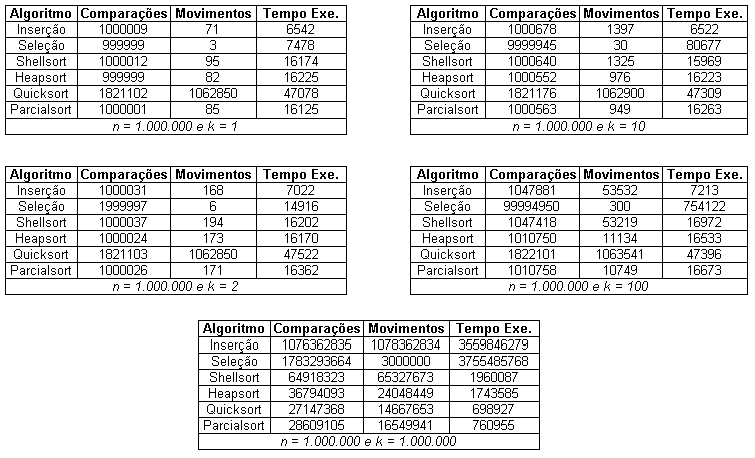
Tabela(17): Algoritmos para ordenação parcial com diferentes tamanhos de k

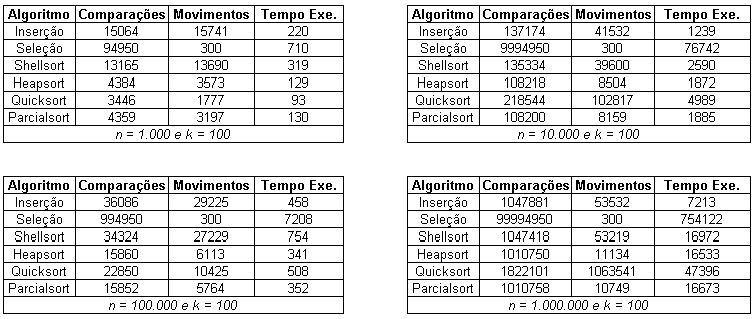
Tabela(18): Algoritmos para ordenação parcial com diferentes tamanhos de n

Nas tabelas (17) e (18) o presente trabalho efetua comparações entre os algoritmos simulados para ordenação parcial. O primeiro resultado observado e já mostrado por Ziviane em [07] para ordenação tradicional foi o excelente desempenho do algoritmo da Seleção para a movimentação de registros O(k), apesar de seu péssimo desempenho no número de comparações. Destaca-se ainda que entre os algoritmos implementados ele foi o que apresentou o pior tempo de execução, seguido pelo algoritmo da inserção. A exceção fica para as situações em que k = 1 e k = 2 em que eles apresentam os menores tempos de execução. Em k = 1, ambos são uma ordem de grandeza menor que os demais algoritmos.

Nota-se que os resultados obtidos para os algoritmos da Inserção e Shellsort foram bem distintos, mesmo eles tendo a segunda parte de seus códigos exatamente iguais. Neste caso, a única explicação possível se dá devido a diferença existente na primeira parte do código. Neste ponto é interessante observar que uma proposta de melhora do algoritmo Shellsort presente neste trabalho seria alterá-lo conforme a proposta do algoritmo original do Shellsort sob o algoritmo da Inserção.

Outro resultado surpreendente, e até mesmo frustrante, foi o resultado da versão do quicksort desenvolvida no presente trabalho. O algoritmo aqui utilizado não se mostrou superior aos demais em termos de tempo de execução. Na maior parte das simulações (execto quando n = k), seu tempo de execução mostrou-se maior que o do Heapsort, o do Shellsort e o do Parcialsort. A explicação para tal resultado é a escolha da chave que não proporcionou que o algoritmo fizesse muitos cortes. Uma proposta de trabalho futuro seria implementar um algoritmo para detecção do k-ésimo elemento e a partir desse, determinar a chave particionadora de forma que na primeira interação todos os n – k elementos maiores seriam excluídos com apenas n – k – 1 comparações. Ainda sobre o quicksort, destaca-se que durante as simulações um fato interessante foi notado: o mesmo além de ordenar os k-ésimos primeiros elementos, ordenava os elementos maiores que k e próximos a esse. Este fato ocorreu devido a natureza do algoritmo e ajuda a explicar o resultado não satisfatório obtido.

Como resultado final tem-se os valores obtidos pelos algorimos Heapsort, o do Shellsort e o do Parcialsort que se alteração, na maior parte das simulações, como os de menor tempo de execução. Entre os três o Parcialsort foi o que apresentou menor número de movimentações de registros, seguido pelo Heapsort. Com relação ao número de comparações, o Heapsort apresentou o melhor resultado, seguido pelo Parcialsort.

Outros Resultados e Código Fonte:

Outros resultado obtidos encontram-se em:

www.dcc.ufmg.br/~maxm/disciplinas/paa/tp/tp1/outrosResultados.xls

O Código Fonte encontra-se em:

www.dcc.ufmg.br/~maxm/disciplinas/paa/tp/tp1/paa.cpp

Uma cópia em formato pdf encontra-se em:

www.dcc.ufmg.br/~maxm/disciplinas/paa/tp/tp1/paa.pdf

Trabalhos relacionados:

The asymptotic complexity of parcial: How to learn large posets by pairwise comparisons

Abstract: The expected number of pairwise comparisons needed to learn a partial order on n elements is shown to be at least n² / 3 – o(n²), and algorithm is given that needs only n² / 4 + o(n²) comparisons on average. In addition, the optimal strategy for learning a poset with four elements is presented.

Bibliografia

[01] - KNUTH, D. E.; “The Art of Computer Programming – volume (1) - Fundamental Algorithms”; Addison-Wesley ; 2^nd edition ; 1997;

[02] - GRAHAM, R., KNUTH, D.. E. and PATASHNIK, O.; “Concrete Mathematics: A Foundation for Computer Science”; Addison-Wesley Publishing Company; 2^nd edition ; 1994

[03] - CORMEN, T. H., LEISERSON C. E. and RIVEST R. L.; “Introduction to Algorithms”; McGraw-Hill ; 1^st edition ; 1990

[04] SEDGEWICK, R.; “Algorithms in C++”; Addison-Wesley; 2^nd edition ; 1988.

[05] - ROSS, K. and WRIGHT C.; “Discrete Mathematics”; Prentice-Hall, Inc.; 3^rd edition; 1992

[06] - KNUTH, D. E.; “The Art of Computer Programming – volume (3) - Sorting and Searching”; Addison-Wesley ; 2^nd edition ; 1997;

[07] - ZIVIANI, N. “Projeto de Algoritmos Com Implementações em Pascal e C”; Pioneira Thomson Learning ; 1993

[08] AZEREDO, P.; “Métodos de Classificação de Dados e Análise de suas Complexidades”; Ed.Campus. Rio de Janeiro; 1996.

[09]- HEITZIG J; “The asymptotic complexity of parcial: How to learn large posets by pairwise comparisons”; May, 2002

[09] - KNUTH, D. E.; “The Art of Computer Programming – volume (2) - Seminumerical Algorithms”; Addison-Wesley ; 2^nd edition ; 1997;

[10] - HOROWITZ, E. and SAHNI, S.; “Fundamentals of Computer Algorithms”; Computer Science Press ; 1978

[11] - CORMEN, T. H., LEISERSON C. E., RIVEST R. L. and STEIN C.; “Introduction to Algorithms”; McGraw-Hill ; 2^nd edition ; 2001