- Bin packing
Resposta:
- Um dos exemplos mais simples que podem ser imaginados é o problema de otimizar a
carga de caminhões no transporte de materiais: dados o volume e o peso de cada unidade
a transportar e a capacidade de cada caminhão, maximizar a carga em cada caminhão para
minimizar a quantidade de caminhões a ser utilizada;
- Um problema curioso pode ser visto em ambientes de processamento paralelo ou
distribuído, onde se dispõe de um certo número de processadores com uma determinada
capacidade (relacionada à carga de trabalho que podem executar) e uma certa quantidade
de trabalhos a serem executados, cada um com uma estimativa de custo de processamento
associada. Dessa forma, o subsistema de controle de tarefas pode alocar os trabalhos
para cada processador, evitando a sobrecarga de alguns deles.

- Um dos exemplos mais simples que podem ser imaginados é o problema de otimizar a
carga de caminhões no transporte de materiais: dados o volume e o peso de cada unidade
a transportar e a capacidade de cada caminhão, maximizar a carga em cada caminhão para
minimizar a quantidade de caminhões a ser utilizada;
- Cobertura de vértices (vertex cover)
Resposta:
- Suponha que um indivíduo esteja planejando suas atividades para o ano seguinte.
Embora tenha vários objetivos em mente (participar de cursos ou conferências, por
exemplo), alguns deles não podem ser feitos ao mesmo tempo, pois os horários conflitam.
A intenção, então, é escolher o maior conjunto de atividades que possam ser feitas sem
que haja qualquer conflito. Ou, remodelando: Ele deseja desistir do menor número
possível de atividades. Ora, se modelarmos a situação através de um grafo onde cada
vértice representa uma atividade e cada aresta representa um conflito, o problema da
cobertura de vértices pode ser utilizado para escolher o menor conjunto possível de
atividades que representem algum conflito.

- Suponha que um indivíduo esteja planejando suas atividades para o ano seguinte.
Embora tenha vários objetivos em mente (participar de cursos ou conferências, por
exemplo), alguns deles não podem ser feitos ao mesmo tempo, pois os horários conflitam.
A intenção, então, é escolher o maior conjunto de atividades que possam ser feitas sem
que haja qualquer conflito. Ou, remodelando: Ele deseja desistir do menor número
possível de atividades. Ora, se modelarmos a situação através de um grafo onde cada
vértice representa uma atividade e cada aresta representa um conflito, o problema da
cobertura de vértices pode ser utilizado para escolher o menor conjunto possível de
atividades que representem algum conflito.
- Mochila (knapsack)
Resposta:
- Dado que uma série de encomendas precisam ser distribuídas, cada uma com uma
prioridade associada, e dado que o meio de transporte - um caminhão, por exemplo -
possui capacidade limitada (de volume ou de peso), um sistema pode modelar esta
situação como o problema da mochila: Carregar ao máximo o caminhão, tentando respeitar
da melhor forma as prioridades das encomendas.

- Dado que uma série de encomendas precisam ser distribuídas, cada uma com uma
prioridade associada, e dado que o meio de transporte - um caminhão, por exemplo -
possui capacidade limitada (de volume ou de peso), um sistema pode modelar esta
situação como o problema da mochila: Carregar ao máximo o caminhão, tentando respeitar
da melhor forma as prioridades das encomendas.
- Subset sum
Resposta:
- Existem alguns estudos acerca do ``problema da compensação bancária'': Um banco
deve compensar valores que saem com valores que entram. Entretanto, esses valores são
fixos (correspondem às movimentações bancárias) e deve-se procurar subconjuntos de
entradas e saídas que se anulem mutuamente, para não gerar pendências de débito ou
crédito entre os bancos. Na realidade, este problema de casamento nada mais é do que
uma maneira diferente de formular o problema de subset sum;
- Alguns pesquisadores sugerem o uso do problema do subset sum - ou melhor,
da sua característica de ser
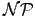 -completo - para construir sistemas de criptografia.
Por exemplo: Armazenar ou transportar senhas em texto puro (plain text) é
considerada prática pouco segura, pois um hacker, tendo acesso ao sistema de
arquivos ou ao canal de comunicação, poderá muito facilmente obtê-las. Uma alternativa
é descrita a seguir: Dado um conjunto fixo de números inteiros
-completo - para construir sistemas de criptografia.
Por exemplo: Armazenar ou transportar senhas em texto puro (plain text) é
considerada prática pouco segura, pois um hacker, tendo acesso ao sistema de
arquivos ou ao canal de comunicação, poderá muito facilmente obtê-las. Uma alternativa
é descrita a seguir: Dado um conjunto fixo de números inteiros 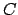 , uma função pode ser
construída de modo a receber como entrada uma palavra-chave - uma senha - e retornar
um subconjunto
, uma função pode ser
construída de modo a receber como entrada uma palavra-chave - uma senha - e retornar
um subconjunto 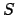 de
de 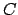 . Assim, bastaria armazenar ou transportar a soma dos
elementos de
. Assim, bastaria armazenar ou transportar a soma dos
elementos de 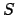 . Embora o valor dessa soma possa tornar-se público, é muito difícil
reconstituir os elementos originais de
. Embora o valor dessa soma possa tornar-se público, é muito difícil
reconstituir os elementos originais de 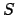 apenas com base nesse valor. Um sistema de
segurança poderá ser construído com confiabilidade suficiente para assegurar que o
único meio de reconstituir o subconjunto
apenas com base nesse valor. Um sistema de
segurança poderá ser construído com confiabilidade suficiente para assegurar que o
único meio de reconstituir o subconjunto 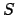 seja digitando novamente a senha que o
originou.
seja digitando novamente a senha que o
originou.

- Existem alguns estudos acerca do ``problema da compensação bancária'': Um banco
deve compensar valores que saem com valores que entram. Entretanto, esses valores são
fixos (correspondem às movimentações bancárias) e deve-se procurar subconjuntos de
entradas e saídas que se anulem mutuamente, para não gerar pendências de débito ou
crédito entre os bancos. Na realidade, este problema de casamento nada mais é do que
uma maneira diferente de formular o problema de subset sum;
- Problema do caixeiro viajante
Resposta:
- Uma rede de computadores pode ser modelada como um grafo completo ponderado: um
pacote de dados pode partir de qualquer nó com destino a outro, e essa operação possui
um custo (tempo) associado. Determinadas aplicações, em particular em ambientes de
processamento distribuído, podem estabelecer que pacotes de controle devem partir de um
determinado nó - um servidor, por exemplo -, viajar por cada nó da rede e retornar ao
ponto de origem. Neste cenário, determinar qual a seqüência mais rápida de nós
diminuirá o tempo total da viagem do pacote.
- Os aparelhos de inserção de componentes em circuitos impressos são programados
para montar uma série de componentes. Se cada ponto de inserção for modelado como um
vértice de um grafo completo e for considerado que a distância entre dois pontos é o
peso associado a cada aresta, então deve-se buscar a seqüência de movimentos que
minimize a distância total percorrida, o que diminui o tempo de fabricação de cada
circuito. O fato de que o caminho é um ciclo fechado advém do fato de que o sistema de
inserção sempre retornará a uma posição inicial após a montagem de cada placa.

- Uma rede de computadores pode ser modelada como um grafo completo ponderado: um
pacote de dados pode partir de qualquer nó com destino a outro, e essa operação possui
um custo (tempo) associado. Determinadas aplicações, em particular em ambientes de
processamento distribuído, podem estabelecer que pacotes de controle devem partir de um
determinado nó - um servidor, por exemplo -, viajar por cada nó da rede e retornar ao
ponto de origem. Neste cenário, determinar qual a seqüência mais rápida de nós
diminuirá o tempo total da viagem do pacote.
O que fazer:
- Prove que este problema é
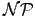 -completo.
-completo.
Resposta: Para provar que um problema é
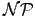 -completo, deve-se provar que ele é
um problema
-completo, deve-se provar que ele é
um problema
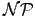 e que é
e que é
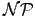 -difícil. As provas serão apresentadas em seguida.
-difícil. As provas serão apresentadas em seguida.
- Prova de que é
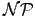 : Um problema é
: Um problema é
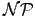 se ele pode ser verificado em
tempo polinomial. Vejamos:
se ele pode ser verificado em
tempo polinomial. Vejamos:
Dado o problema de decisão relacionado, enunciado a seguir:
``Dado um grafo não orientado completo ponderado
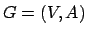 , determinar se um certo
caminho
, determinar se um certo
caminho
 percorre uma distância menor
ou igual a um valor
percorre uma distância menor
ou igual a um valor 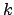 , sendo
, sendo
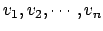 cada um dos vértices do conjunto
cada um dos vértices do conjunto
 , em qualquer ordem.''
, em qualquer ordem.''
A solução para este problema pode ser modelada pelo pseudo-código a seguir, onde
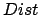 é a matriz de adjacência:
é a matriz de adjacência:
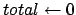 ;
;
Para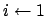 até
até 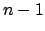 Faça
Faça
![$ total \leftarrow total + Dist[v_i, v_{i+1}]$](img18.gif) ;
;
![$ total \leftarrow total + Dist[v_n, v_1]$](img19.gif) ;
;
Retorne ;
;
De fato, este algoritmo é executado em tempo polinomial - mais especificamente, em
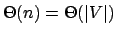 . Portanto:
. Portanto:
- Prova de que é
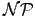 -difícil: Para isto, deve-se tomar um problema
reconhecidamente
-difícil: Para isto, deve-se tomar um problema
reconhecidamente
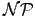 -difícil e criar uma maneira de reduzi-lo polinomialmente ao PCV.
Aqui, parte-se do Problema do Ciclo Hamiltoniano (PCH), reconhecidamente
-difícil e criar uma maneira de reduzi-lo polinomialmente ao PCV.
Aqui, parte-se do Problema do Ciclo Hamiltoniano (PCH), reconhecidamente
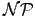 -difícil, e
será demonstrada uma redução ao PCV.
-difícil, e
será demonstrada uma redução ao PCV.
Dada uma instância
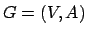 para o PCH, deve-se construir um grafo
para o PCH, deve-se construir um grafo
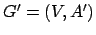 ,
onde, para cada aresta
,
onde, para cada aresta
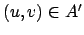 , temos que o custo
, temos que o custo 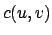 dessa aresta é
dessa aresta é
Além disto, o grafo
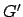 é completo, ou
é completo, ou
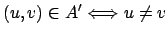
A partir deste ponto,
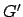 pode ser uma instância para o PCV: é um grafo completo,
ponderado e bem definido. Para fechar a questão, deve-se provar que: (i) a redução pode
ser feita em tempo polinomial; (ii)
pode ser uma instância para o PCV: é um grafo completo,
ponderado e bem definido. Para fechar a questão, deve-se provar que: (i) a redução pode
ser feita em tempo polinomial; (ii) 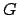 tem solução para o PCH somente se
tem solução para o PCH somente se 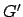 tem
solução para o PCV com custo máximo 0; e (iii) vice-versa -
tem
solução para o PCV com custo máximo 0; e (iii) vice-versa - 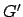 tem solução para o
PCV com custo máximo 0 somente se
tem solução para o
PCV com custo máximo 0 somente se 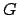 tem solução para o PCH.
tem solução para o PCH.
- A redução pode ser feita em tempo polinomial: Testar todos os pares de
vértice
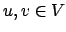 para determinar o custo de
para determinar o custo de 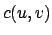 demanda tempo
demanda tempo 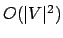 .
Além disto, para uma implementação eficiente - digamos, por matriz de adjacências
-, tanto checar a existência de
.
Além disto, para uma implementação eficiente - digamos, por matriz de adjacências
-, tanto checar a existência de 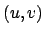 em
em 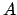 quanto armazenar o custo
quanto armazenar o custo 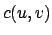 demandam tempo
demandam tempo 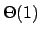 . Portanto, a redução tem complexidade polinomial.
. Portanto, a redução tem complexidade polinomial.
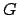 tem solução para o PCH somente se
tem solução para o PCH somente se 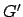 tem solução para o PCV com
custo máximo 0: Se for encontrada uma solução para o PCV com custo máximo 0 - e
dado que não há arestas com custo negativo -, então todas as arestas do ciclo
encontrado possuem custo 0. Entretanto, pela regra de formação das arestas de
tem solução para o PCV com
custo máximo 0: Se for encontrada uma solução para o PCV com custo máximo 0 - e
dado que não há arestas com custo negativo -, então todas as arestas do ciclo
encontrado possuem custo 0. Entretanto, pela regra de formação das arestas de 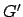 apresentada em (2), nota-se que cada aresta de custo 0 em
apresentada em (2), nota-se que cada aresta de custo 0 em 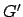 corresponde a uma aresta existente em
corresponde a uma aresta existente em 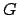 . Portanto, se houver solução para o PCV,
então existe um ciclo hamiltoniano em
. Portanto, se houver solução para o PCV,
então existe um ciclo hamiltoniano em 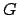 .
.
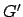 tem solução para o PCV com custo máximo 0 somente se
tem solução para o PCV com custo máximo 0 somente se 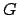 tem
solução para o PCH: Se houver um ciclo hamiltoniano em
tem
solução para o PCH: Se houver um ciclo hamiltoniano em 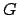 , então ele é formado
por uma série de arestas
, então ele é formado
por uma série de arestas
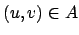 . Mas, pela regra de redução definida em
(2), cada uma dessas arestas torna-se uma aresta de custo 0 em
. Mas, pela regra de redução definida em
(2), cada uma dessas arestas torna-se uma aresta de custo 0 em
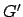 , que também formam um ciclo - e, portanto, uma solução para o PCV de custo 0.
, que também formam um ciclo - e, portanto, uma solução para o PCV de custo 0.
Com base nas três provas apresentadas, deduzimos então que
- A redução pode ser feita em tempo polinomial: Testar todos os pares de
vértice
Finalmente, com base nas deduções (1) e (3), concluímos que o Problema do Caixeiro Viajante é
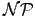 -completo.
-completo.

- Prova de que é
- Implemente um algoritmo capaz de obter a solução ótima para este problema.
Informe o tamanho do maior problema que você conseguiu obter a solução ótima. Comente o
resultado indicando o motivo da limitação e faça uma estimativa do tempo necessário no caso
de termos uma entrada 10 vezes maior que a do maior problema que voce resolveu.
Sobre o algoritmo: O algoritmo implementado é bastante simples. Basicamente, é uma adaptação do algoritmo de pesquisa primeiro em profundidade (Depth-First Search), com duas alterações básicas:
- Ao visitar todos os vizinhos de um determinado vértice, ele é novamente pintado
de branco, para que possa ser visitado posteriormente, fazendo parte de novos caminhos.
Isto impede que sejam geradas árvores com ramificações: apenas caminhos simples;
- Quando a visita tiver chegado à sua profundidade máxima, calcula-se o custo
total do ciclo obtido (arestas da árvore caminhada + aresta que liga o último ao
primeiro vértice), comparando-o com o melhor resultado obtido até o momento e
armazenando este ciclo, caso este seja ainda melhor.
Maior problema resolvido: O maior problema que se conseguiu resolver possui 14 vértices e demorou pouco mais de 28 minutos para ser processado. O problema com 15 vértices foi interrompido após cerca de 3 horas, tendo sido considerado insolúvel em tempo razoável para a plataforma de execução adotada.
É importante ressalvar que esses tempos foram conseguidos sem qualquer otimização sobre o algoritmo de força bruta. Especificamente, não foi implementada a checagem de limite de distâncias percorridas, que permite que uma determinada tentativa seja interrompida caso se perceba que ela necessariamente levará a uma solução pior do que a que foi encontrada até o momento. Isto porque uma implementação desse tipo influenciaria a cronometragem, pois é possível que a instância proposta seja particularmente boa ou ruim para esta abordagem.
A Tabela 1 sumariza os tempos obtidos com as execuções do algoritmo adotando quantidades crescentes de vértices.
Projeção de tempo para uma entrada dez vezes maior do que a do maior problema resolvido: É muito interessante plotar os tempos obtidos em um gráfico logarítmico na ordenada, que nos dá uma boa noção do comportamento do crescimento de tempo em função do número de vértices:
De fato, há uma conformação exponencial no crescimento da função de tempo. A resolução da questão proposta é feita em três passos:
- Tomando o eixo das ordenadas como sendo linear (usando o logaritmo do tempo),
temos a seqüência de dados vista na Tabela 2;
Tabela 2: Logaritmo dos tempos obtidos N^o vértices 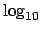 (Tempo)
(Tempo)8 0 9 0,903089987 10 1,913813852 11 2,938019097 12 4,005309237 13 5,09972897 14 6,22913383
- Usando o Método dos Mínimos Quadrados, adaptamos estes dados à equação de uma reta:
onde
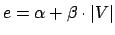 e
e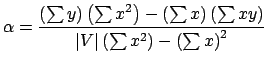
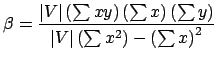
Dessas equações obtemos os valores de
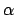 e
e 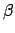 :
:
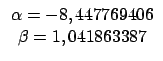
- Adota-se como projeção de tempo
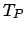 a seguinte equação exponencial:
a seguinte equação exponencial:
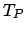
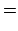
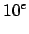
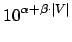
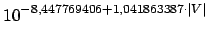
Para observar a veracidade da equação proposta, a Figura 2 sobrepõe a plotagem dos tempos projetados (linha sólida vermelha) aos tempos obtidos (linha tracejada azul), demonstrando uma conformação bastante adequada.
Figura 2: Plotagem logarítmica da projeção de tempo (linha sólida) sobre os tempos obtidos (linha tracejada) Finalmente, o resultado da questão: Basta calcular o valor de
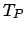 para
para 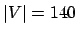 :
:
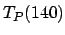
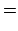
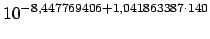
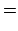
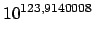
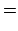
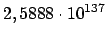 ms
ms
o que é um tempo completamente fora de qualquer ordem de grandeza imaginável pelo ser humano. Convertendo, por exemplo, este tempo em milênios, teríamos- outro número igualmente impossível de ser compreendido.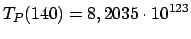 milênios
milênios
- Ao visitar todos os vizinhos de um determinado vértice, ele é novamente pintado
de branco, para que possa ser visitado posteriormente, fazendo parte de novos caminhos.
Isto impede que sejam geradas árvores com ramificações: apenas caminhos simples;
- Implemente uma heurística (ou aproximação) que resolva este problema
eficientemente e produza ``boas'' soluções sob o ponto de vista prático. Apresente uma
análise de complexidade de tempo da sua heurística. Use a matriz disponível aqui:
http://www.dcc.ufmg.br/
 nivio/cursos/pa03/tp2/matriz-de-entrada. Imprima o
caminho obtido e seu custo. As melhores soluções vão ser premiadas com pontos extras. Mais
especificamente, as 5 melhores soluções que sejam até 10% piores (em termos do custo do
caminho encontrado) que a melhor obtida.
nivio/cursos/pa03/tp2/matriz-de-entrada. Imprima o
caminho obtido e seu custo. As melhores soluções vão ser premiadas com pontos extras. Mais
especificamente, as 5 melhores soluções que sejam até 10% piores (em termos do custo do
caminho encontrado) que a melhor obtida.
Descrição do algoritmo: O algoritmo implementado é uma simplificação do algoritmo de Christofides, com a aplicação de um algoritmo de melhoramento de resultados por permutação de vértices.
Basicamente, o algoritmo proposto funciona da seguinte maneira:
- A partir do grafo ponderado fornecido como base do problema, obtém-se uma Árvore
Geradora Mínima (um conjunto de arestas
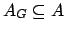 );
);
- Usa-se os vértices de grau ímpar para obter um matching (um conjunto de
arestas
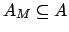 );
);
- A partir do caminho euleriano formado pelos vértices
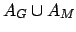 , constrói-se
uma solução para o PCV realizando o caminhamento com curto-circuitos (isto é, saltando
todo vértice que já tiver sido visitado).
, constrói-se
uma solução para o PCV realizando o caminhamento com curto-circuitos (isto é, saltando
todo vértice que já tiver sido visitado).
A diferença entre este algoritmo e o proposto por Christofides está no passo (ii). Enquanto Christofides estabelece o uso do matching mínimo, neste algoritmo deciciu-se pelo uso de um algoritmo guloso, descrito a seguir:
- Coleta-se o conjunto de vértices
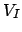 de grau ímpar;
de grau ímpar;
- Coleta-se o conjunto de todas as arestas
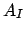 que liguem pares de vértices em
que liguem pares de vértices em
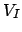 ;
;
- Faz-se a escolha da aresta
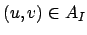 de menor custo, onde
de menor custo, onde
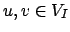 ;
;
- Retira-se as arestas
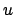 e
e 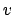 do conjunto
do conjunto 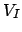 ;
;
- Repete-se os passos (iii) e (iv) até que
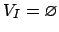 .
.
Este algoritmo guloso, apesar de ser executado em tempo bem menor do que o matching mínimo, evidentemente não garante a obtenção do melhor resultado possível.
O algoritmo de melhoramento aplicado ao final consiste dos seguintes passos:
- A partir do melhor caminho
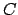 obtido após a execução do algoritmo principal
(descrito anteriormente), toma-se
obtido após a execução do algoritmo principal
(descrito anteriormente), toma-se 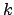 vértices distintos;
vértices distintos;
- Realiza-se todas as permutações possíveis desses vértices dentro do arranjo
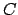 ,
calculando, para cada uma das
,
calculando, para cada uma das 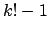 permutações1, a nova distância total e verificando se esta
é melhor do que a obtida originalmente;
permutações1, a nova distância total e verificando se esta
é melhor do que a obtida originalmente;
- Repetem-se os passos anteriores para cada conjunto distinto de
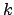 vértices.
vértices.
Este pequeno algoritmo de melhoramento é capaz de aprimorar sensivelmente os resultados obtidos. Para o programa escrito, adotou-se
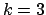 .
.
Análise de complexidade: Um bom critério para analisar a complexidade deste algoritmo está em contabilizar o número de comparações de custos de arestas. De fato, ao observar o código-fonte do programa, é possível observar que esta operação ocorre em todas as recursões e em todos os laços relevantes da implementação.
As rotinas do módulo priorqueue.c abstraem a comparação de chaves através de chamadas a função Compare( ). Este módulo representa a implementação padrão de heaps para filas de prioridades, portanto pode-se adotar a análise tradicional vista em Cormen [1] para as rotinas de manutenção do heap. Isto porque a operação de comparação é determinante para o tempo de execução de todas as rotinas deste módulo. Assim, temos:
- PriorQueueMinHeapify( ):
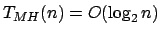
- PriorQueueBuildMinHeap( ):
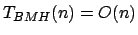
- PriorQueueExtractMin( ):
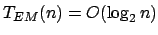
- PriorQueueDecreaseKey( ):
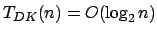
As rotinas do módulo heuristica.c que compõem a estrutura do algoritmo são analisadas em seqüência:
- heuristProcuraCiclo( ): Para cada iteração do laço principal, a rotina
descobre uma aresta de cor branca que liga o vértice 'u' a um vértice 'v'. A procura
deste vértice é feita em
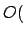 nSizead
nSizead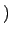 comparações - linhas 171-186. A aresta
encontrada é pintada de cinza, e o laço principal repete-se até que não seja mais
possível encontrar arestas brancas. Como a cada iteração uma aresta é pintada de cinza,
então o laço principal é executado
comparações - linhas 171-186. A aresta
encontrada é pintada de cinza, e o laço principal repete-se até que não seja mais
possível encontrar arestas brancas. Como a cada iteração uma aresta é pintada de cinza,
então o laço principal é executado
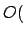 nSizead
nSizead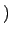 vezes. Portanto, a complexidade
desta rotina é
O pior caso para 'nSizead' é quando todos os vértices têm grau ímpar e, portanto, o número de arestas consideradas é o dobro do número de vértices. Portanto, pode-se dizer que
vezes. Portanto, a complexidade
desta rotina é
O pior caso para 'nSizead' é quando todos os vértices têm grau ímpar e, portanto, o número de arestas consideradas é o dobro do número de vértices. Portanto, pode-se dizer que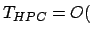 nSizead
nSizead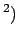
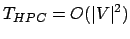
- heuristProcuraCicloTotal( ): Não há comparação de chaves nesta rotina,
apenas chamadas a heuristProcuraCiclo( ). A primeira chamada a
heuristProcuraCiclo( ) descobre um ciclo, que percorrerá pelo menos 2 vértices.
Cada chamada adicional a heuristProcuraCiclo( ) adiciona um novo sub-ciclo ao
ciclo original, ou seja, adiciona pelo menos 1 vértice a cada iteração (laço das linhas
219-247). Assim, no pior caso são feitas
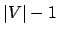 chamadas a
heuristProcuraCiclo( ). Portanto, a complexidade de
heuristProcuraCicloTotal( ) é
chamadas a
heuristProcuraCiclo( ). Portanto, a complexidade de
heuristProcuraCicloTotal( ) é
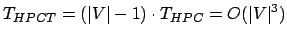
- calcDistCaminho( ): Não há comparações feitas nesta rotina, portanto:
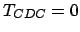
- procCaminhoHeuristica( ): A linha 313 consome
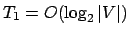 . O
laço das linhas 330-355 consome:
. O
laço das linhas 330-355 consome: 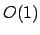 comparação (linha 336) mais
comparação (linha 336) mais
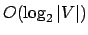 (linha 352) comparações. Como este laço é executado
(linha 352) comparações. Como este laço é executado 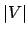 vezes, temos que o seu custo
é de
vezes, temos que o seu custo
é de
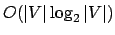 comparações. O laço imediatamente externo, das linhas 316-356,
engloba este custo mais
comparações. O laço imediatamente externo, das linhas 316-356,
engloba este custo mais
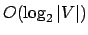 (linha 320) e é executado no máximo
(linha 320) e é executado no máximo 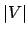 vezes
(até exaurir a fila de prioridades de vértices 'vdpq'). Portanto, o custo das linhas
316-356 é
vezes
(até exaurir a fila de prioridades de vértices 'vdpq'). Portanto, o custo das linhas
316-356 é
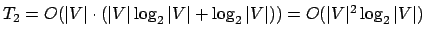 .
.
O laço das linhas 367-378 não realiza nenhuma comparação de chaves, nem o laço das linhas 391-399. Já o laço das linhas 404-419 é executado no máximo duas vezes o número de vértices ímpares, que por sua vez é no máximo o número de vértices; o único comando relevante é o da linha 405, que executa
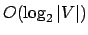 comparações; portanto, o máximo
possível de comparações do laço é igual a
comparações; portanto, o máximo
possível de comparações do laço é igual a
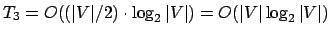 .
.
As linhas 433-472 correspondem a três laços aninhados, e cada iteração interna (linhas 438-469) chama 5 vezes a rotina calcDistCaminho( ); entretanto, como o seu custo em comparações é
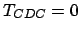 , estes laços aninhados não contam comparações.
, estes laços aninhados não contam comparações.
Finalmente, todos esses passos estão incluídos em um grande laço externo (linhas 296-476) que é executado
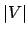 vezes. Portanto, o custo total da heurística, em termos
de comparações de chaves, é
vezes. Portanto, o custo total da heurística, em termos
de comparações de chaves, é
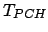
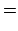
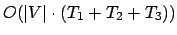
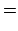
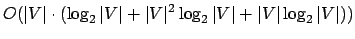
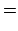

Melhor caminho obtido: De acordo com a heurística proposta, o caminho mais curto encontrado para a instância do problema brazil58 foi:
 20, 28, 35, 16, 25, 5, 18, 27, 13, 36, 33, 14, 45, 55, 44, 32, 7,
21, 54, 53, 1, 40, 47, 2, 34, 9, 51, 50, 46, 48, 42, 26, 4, 22, 11, 56, 23, 57, 43, 17, 0,
29, 12, 39, 24, 8, 31, 19, 52, 49, 3, 6, 30, 37, 41, 15, 10, 38, 20
20, 28, 35, 16, 25, 5, 18, 27, 13, 36, 33, 14, 45, 55, 44, 32, 7,
21, 54, 53, 1, 40, 47, 2, 34, 9, 51, 50, 46, 48, 42, 26, 4, 22, 11, 56, 23, 57, 43, 17, 0,
29, 12, 39, 24, 8, 31, 19, 52, 49, 3, 6, 30, 37, 41, 15, 10, 38, 20
Este caminho percorre uma distância de 27.024 unidades - cerca de 6,41% maior do que o melhor caminho encontrado até hoje, de 25.395 unidades.

- A partir do grafo ponderado fornecido como base do problema, obtém-se uma Árvore
Geradora Mínima (um conjunto de arestas
- Apresente uma análise indicando o quanto a solução heurística fornecida
aproxima-se do resultado ótimo (você pode explicar resultados encontrados na literatura ou
ainda apresentar sua própria demonstração).
Resposta: Para realizar esta análise, algumas convenções serão estabelecidas:
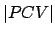
é o custo do caminho ótimo do PCV; 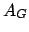
é o conjunto de arestas que compõem a Árvore Geradora Mínima; 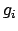
é cada uma das arestas pertencentes a 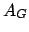 , com
, com
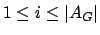 ;
;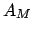
é o conjunto de arestas que compõem o matching; 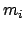
é cada uma das arestas pertencentes a 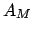 , com
, com
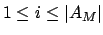 .
.Considere a AGM formada pelas arestas
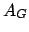 . A soma dos custos de cada uma destas arestas é
menor do que o custo do caminho ótimo para o PCV, ou
. A soma dos custos de cada uma destas arestas é
menor do que o custo do caminho ótimo para o PCV, ou
Analisando agora as arestas
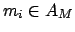 : Pela desigualdade de triângulos, cada aresta
: Pela desigualdade de triângulos, cada aresta
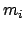 não pode ser maior do que o correspondente segmento da solução ótima para o PCV,
portanto
não pode ser maior do que o correspondente segmento da solução ótima para o PCV,
portanto
Ao considerar a união das arestas de
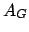 e
e 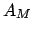 , obtém-se um caminho euleriano cujo
custo é
, obtém-se um caminho euleriano cujo
custo é
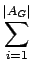 Custo
Custo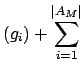 Custo
Custo
Como este caminho será percorrido fazendo-se curto-circuitos, espera-se que no caso médio sejam obtidos resultados bem melhores do que
 .
.

- Realize testes com entradas escolhidas aleatoriamente e compare os resultados
com a análise de eficiência apresentada no item anterior. Comente os resultados obtidos e
discuta o quão próxima a análise teórica está da realidade.
Testes realizados: Foi realizado um experimento com 1.000 entradas aleatoriamente geradas de instâncias com 10 vértices2. Os experimentos constaram em executar a heurística e comparar seus resultados (custo total dos caminhos) com o obtido através da força bruta. Os resultados obtidos foram interessantes, pois demonstram a eficiência do algoritmo obtido:
- Em 63,9% (quase 2/3) dos casos, a heurística foi capaz de determinar o caminho
ótimo;
- No pior caso, o caminho descoberto foi apenas 16,09% mais longo do que o caminho
ótimo;
- Os caminhos encontrados foram em média 1,44% mais longos do que os caminhos
ótimos.
Pela tabela de distribuição abaixo, é possível observar que em quase 80% dos casos a heurística apresentada é capaz de obter soluções apenas 2,5% piores em relação ao caminho ótimo:

Comentários: Analisando os dados apresentados acima, é possível perceber que, no caso esperado, a expectativa é de conseguir resultados bem melhores do que o limite calculado de
 (discutido na Questão (d)). Mesmo o pior caso que ocorreu é
muito distante deste limite. Os seguintes motivos podem ser apontados para este fato:
(discutido na Questão (d)). Mesmo o pior caso que ocorreu é
muito distante deste limite. Os seguintes motivos podem ser apontados para este fato:
- A análise toma por base o limite superior de
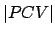 para a soma das distâncias
das arestas da Árvore Geradora Mínima (Eq. (4)), quando sabe-se que
esta soma é menor;
para a soma das distâncias
das arestas da Árvore Geradora Mínima (Eq. (4)), quando sabe-se que
esta soma é menor;
- A escolha gulosa para as arestas que compõem o matching, embora não
garanta um resultado ótimo, tende a chegar a bons resultados, obtendo um conjunto de
arestas cuja soma dos pesos não deve chegar perto de
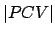 (limite segundo a
Eq. (5));
(limite segundo a
Eq. (5));
- O caminhamento com curto-circuitos reduz drasticamente a distância percorrida,
pois vários segmentos são substituídos por uma única aresta;
- Finalmente, o algoritmo de melhoramento final por permutação de vértices traz
resultados ainda mais próximos do ideal3.

- Em 63,9% (quase 2/3) dos casos, a heurística foi capaz de determinar o caminho
ótimo;
- Submeta eletronicamente a implementação da solução ótima utilizando como
entrada de dados a seguinte matriz:
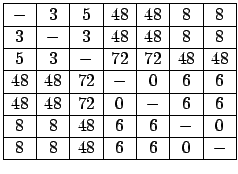
Resposta: O caminho mais curto encontrado é
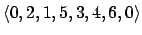 , percorrendo uma distância de 36 unidades.
, percorrendo uma distância de 36 unidades.

- Apresente a documentação das implementações realizadas (veja aqui maiores
detalhes sobre instruções para a entrega de trabalhos praticos:
http://www.dcc.ufmg.br/
 nivio/cursos/pa03/entrega).
nivio/cursos/pa03/entrega).
Resposta: Apresentada na Seção 2.

