para o problema brazil58, o melhor resultado já encontrado e publicado pela TSPLIB.
- Palavras-chave
- Problema do Caixeiro Viajante, Heurísticas, Otimização, Performance de Pior Caso, STSP, TSPLIB.
Luciano Bertini
2
Universidade Federal de Minas Gerais
Departamento de Ciência da Computação
16 de Junho de 2003
para o problema brazil58, o melhor resultado já encontrado e publicado pela TSPLIB.
for the problem brazil58, the best result
ever published by TSPLIB.
cidades para a submissão eletrônica
Apresente pelo menos um exemplo prático (e não mais do que três) que possa ser modelado através dos seguintes problemas:
A formulação do problema Bin Packing é dada da seguinte forma
por [GJ79]: Dado um conjunto finito
de itens e um tamanho racional ![$s(u)\in[0,1]$](img4.png){kind=small}
para cada item 
,
encontre um particionamento de 
em subconjuntos disjuntos
tal que a soma dos tamanhos dos itens de cada 
não seja maior
que 
e tal que 
seja mínimo. Um subconjunto pode
ser visto como um conjunto de itens a ser colocado em uma célula de
capacidade 1 (bin), onde o objetivo é empacotar os itens de no
menor número possível de células (bins). A figura 1 ilustra
o problema.
Uma possível aplicação do problema Bin Packing é na alocação
de largura de banda em redes de alta velocidade. Em [KRT97],
é feito um estudo da multiplexação estatística através de algoritmos
heuristicos. Em redes de alta velocidade, conexões individuais são
do tipo rajada, com taxas de dados que variam muito no tempo. Assim,
o problema de empacotar múltiplas conexões em um único link de largura
de banda definido recai sobre o problema Bin Packing. Na abordagem do problema,
a capacidade do link e uma probabilidade
de overflow permitido são dados, e o objetivo é estabelecer conexões
de forma que a probabilidade da carga exceder a capacidade do link
seja no máximo .
Uma segunda aplicação do problema Bin Packing é na modelagem de escalonamento de processos em um sistema paralelo. Em [BLOS94], é abordado o caso específico de sistemas de tempo real. A única diferença do problema de escalonamento de processos para o problema bin-packing é que os pacotes do bin-packing são de tamanho unitário, enquanto que no escalonamento de processos, o tamanho ou utilização do processador muda dinamicamente de acordo com uma função pré-definida, no caso de algoritmos dinâmicos, como apresentado em [OS93].
A definição deste problema dada por [GJ79] é como segue.
Uma instância do problema é um grafo 
e um número inteiro
. O problema consiste em responder a seguinte
questão: existe uma cobertura de vértice de tamanho 
ou menos
para 
, isto é, um subconjunto
tal que
e, para cada vértice
, pelo menos um,
ou 
, pertence a 
? A figura 2 ilustra
através de um grafo com destaque de .
Uma ablicação bastante prática e específica encontrada foi a apresentada em [SM96], na área de microeletrônica. Os dispositivos internos de um chip são conectados por linhas e colunas que devem ser alocadas para tal. Esse problema de alocação pode ser resolvido com base no problema da cobertura de vértices, pois o objetivo é alocar de maneira ótima as linhas e colunas, salvando espaço e performance. O artigo apresenta como exemplo circuitos reparadores de memória que não embutem overhead significativo, devido à otimização.
Um problema interessante apontado por [LP98] (pág. 269) seria numa situação em que se deseja destacar o mínimo possível de guardas para um conjunto de salas (Aplicação de um vestibular, por exemplo), de modo que todos os corredores possam ser vigiados por um guarda.
Outras aplicações do problema da cobertura de vértices estão relacionadas com a solução de outros problemas através de uma transformação polinomial. Um exemplo é a transformação para um conjunto independente de vértices ou para o problema da coloração de grafos ([GJ79] pág. 133).
Definição do problema [GJ79]: seja um conjunto
finito onde cada possui um tamanho inteiro positivo 
e um valor 
também inteiro positivo, além de dois inteiros
e . Existe algum subconjunto
tal que
e tal que
?
No artigo [VH01], é apresentada uma aplicação do problema knapsack para a solução do problema de escalonamento de fotografias tiradas diariamente por um satélite de observação da Terra. Esse problema é referido como Daily Photograph Scheduling Problem (DPSP) na literatura da área. O principal objetivo do DPSP é escalonar um subconjunto de fotografias a partir de um conjunto de candidatas que serão efetivamente tiradas pelo satélite. O subconjunto de fotografias resultante deve satisfazer um grande número de restrições e ao mesmo tempo maximizar uma dada função custo. O artigo em questão introduz uma formulação para o DPSP usando o conhecido 0/1 Knapsack e em seguida desenvolve uma heurística baseada na técnica Tabu Search (TS).
Uma outra aplicação antiga do problema Knapsack foi na área da criptografia. O primeiro sistema criptográfico baseado no problema knapsack foi proposto por Merkle & Hellman. O artigo [Odl91] mostra como esse sistema pôde ser quebrado. Apesar do declínio desse método, a criptografia modelada pelo problema Knapsack ainda é estudada.
Definição do problema [GJ79]: seja um conjunto 
finito onde cada 
possui um tamanho inteiro positivo 
e um inteiro positivo . Existe algum subconjunto
tal que
?
Como exemplo de aplicação, considere o seguinte problema: um conjunto
de arquivos precisa ser armazenado em um disco de tamanho 
.
O tamanho do i-ésimo arquivo é 
e o tamanho total de todos
os arquivos é maior que o tamanho do disco. Quais arquivos devem ser
salvos para ficar o mais próximo possível de ocupar todo o disco?
Mais formalmente, existe algum subconjunto de arquivos
tal que
?
O livro [Rei94] traz uma lista não exaustiva de aplicações para o problema do Caixeiro Viajante. Uma das mais clássicas é na confecção de Placas de Circuito Impresso (PCB), na tarefa de perfuração. Uma placa de circuito impresso pode conter centenas ou milhares de furos, que são feitos para a soldagem dos componentes eletrônicos. Além disso, os furos podem ser de tamanhos diferentes. Para otimizar o processo, deve-se perfurar todos os furos de mesmo diâmetro por vez, já que a troca da ferramenta é um processo relativamente lento. Assim, a perfuração pode ser vista como uma seqüência de problemas do Caixeiro Viajante. Percorrendo-se o melhor caminho possível, economiza-se tempo, aumentando a produtividade do processo.
Uma segunda aplicação apresentada na mesma referência do exemplo anterior,
é a que ocorre na análise de estruturas de cristais na cristalografia
por Raios-X. Um difratômetro de Raios-X é usado para obter informações
sobre a estrutura de materiais cristalinos. Um detector mede a intensidade
dos Raios-X refletidos do material, saindo de várias posições. Em
alguns experimentos, o detector deve realizar até 
deslocamentos
para fazer as medidas. O movimento é feito através de quatro motores
e o tempo gasto para um movimento é conhecido com precisão. Como a
seqüência de realizações das medidas é irrelevante para o experimento,
para minimizar o tempo gasto, deve-se escolher um percurso mínimo
entre os pontos de medida, o qual pode ser modelado através
de um TSP.
e uma distância 
para cada par de cidades
,
encontre o ``roteiro'' para todas as cidades em 
cujo comprimento total seja o menor possível.
Este problema é conhecido na literatura como o problema do caixeiro viajante (PCV).
Para efetuarmos a prova, primeiro temos que provar que o problema
STSP está em 
. Para isso, vamos mostrar que existe um
algoritmo determinístico polinimial que seja capaz de verificar se
uma determinada seqüência de vértices é ou não é uma solução para
o problema. Então vamos usar o valor que seria o limite superior
para o tamanho do ciclo. Seja o conjunto de cidades
e seja
a distância entre as cidades 
e 
. O algoritmo 1 verifica se uma determinada seqüência
de cidades
é uma solução, ou seja,
verivica se o comprimento do ciclo definido por T é menor que .
Como o algoritmo 1 é 
, fica provado que o problema do Caixeiro Viajante Simétrico é .
Para provarmos que STSP é um problema
, vamos provar que existe uma transformação polinomial do problema
do ciclo Hamiltoniano para o problema STSP, pois já é conhecido que o ciclo Hamiltoniano é
[LP98]
- pág. 303.
Dado um grafo simétrico , onde o conjunto de vértices é
, construiremos a seguinte instância do problema STSP:
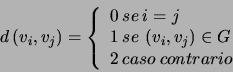
Como o grafo é simétrico e sem laços, essa função é também simétrica,
o que significa dizer que
para todas as cidades 
e 
. Por fim, o custo mínimo
da viagem é exatamente 
, passando por todas as arestas de custo .
Qualquer ciclo terá custo igual a mais o número de distâncias entre as cidades percorridas
que não estão nas arestas de . Portanto, um ciclo de custo ou menos existe se e somente se
o número de ``não arestas'' utilizado é zero, isto é, se e somente se o ciclo é um ciclo Hamiltoniano de .
A técnica utilizada para a criação do algoritmo ótimo foi baseada no algoritmo de busca em profundidade em grafos (Depth First Search - DFS), porém fazendo uma modificação para que sempre que uma busca termine, o último vértice visitado é marcado como inexplorado, permitindo que todas as combinações de caminhos sejam experimentadas.
A referência de implementação adotada foi a do algoritmo DFS apresentado em [MTG02], que armazena apenas dois estados para os vértices e arestas: explorado ou inexplorado, diferentemente do algoritmo DFS apresentado em [Cor01] com três estados possíveis marcados pelas cores branco, cinza ou preto. O algoritmo 2 já é o algoritmo modificado para percorrer em profundidade todos os caminhos possíveis.
. A tabela 1 mostra os resultados obtidos.
Os tempos foram medidos com a função time do Unix.
|
O comando uname -a retornou:
diamante:~->uname -a SunOS diamante 5.5.1 Generic_103640-40 sun4m sparc sun4m
A análise de complexidade do algoritmo é bem simples. O algoritmo realiza todas as permutações possíveis, ou seja,
. Para cada uma delas, o algoritmo invoca a função 
que executa operações de soma. Portanto,
o número de operações de soma realizadas é 
.
Os resultados obtidos foram os esperados. A limitação de 
em
apenas 
ocorreu porque o número de operações a serem realizadas pela execução com 
seria 
vezes maior, o que
resultaria em aproximadamente 
horas. Devido ao prazo curto para a entrega deste trabalho, não foi possível esperar
esse tempo.
É portanto fácil estimar o tempo para um dado valor de . Será igual a vezes o tempo que levou para executar para 
.
O tempo estimado é dado pela seguinte expressão:
onde é um valor para o qual o tempo de execução 
é conhecido e 
é o tempo estimado
para um tamanho N. Com essa expressão, todas as constantes multiplicativas ficam embutidas, sem que seja necessário calculá-las.
então, temos:
Da tabela 1, temos que
segundos. Um cálculo aproximado dos fatoriais
resulta:
e
.
substituindo, obtemos:
que resulta em:
segundos
minutos
horas
dias
anos
séculos
milênios
A heurística de construção do vértice mais distante funciona da seguinte maneira: escolha o vértice mais distante do ciclo atual e em seguida insira-o no ciclo atual na posição que resultar no menor custo. Existem algumas variações desse algoritmo, por exemplo, inserir a aresta cuja distância mínima ao ciclo atual seja máxima; ou inserir o vértice cuja máxima distância ao ciclo atual seja mínima; ou ainda simplesmente inserir o vértice cuja distância ao ciclo atual seja máxima. Essas três variantes são apresentadas em [Rei94]. A variante implementada foi a que insere o vértice cuja distância mínima seja máxima. O algoritmo está descrito a seguir (algoritmo 3).
A heurística da inserção mais distante mostrou-se surpreendentemente boa. Em todos a literatura, esse algorítmo demonstra ser melhor que os demais algoritmos de inserção, bem como o do visinho mais próximo, chegando às vezes a bater o algoritmo da árvore geradora mínima de Cristofides. O segredo está no fato que ao se inserir a aresta mais distante, o algoritmo não cai em mínimos locais que atrapalham a busca. Na execução do algoritmo, para obter um ciclo melhor, foi executado a partir de cada ciclo inicial possível.
Em seguida, foi realizada uma implementação bastante simples do algorítmo de melhoria 2-opt [Rei94]. O algoritmo 2-opt consiste em se eliminar duas aresta do ciclo e inseri-las novamente de forma cruzada, caso isso melhore o ciclo. A figura ZZZ mostra como é feito um movimento 2-opt.
O algoritmo implementado consiste em testar cada combinação possível
de movimentação e verificar se há alguma melhoria. Esse é o algorítmo
2opt. Uma observação feita foi que após a verificação das 
combinações,
um flip pode deixar para trás a necessidade de uma inversão. Então
foi feito um loop mais exeterno que repete as combinações
até que em uma passada completa, nenhuma modificação seja feita. Observou-se
que o número de iterações desse loop é oscila mas é um número 
.
Para implementar um movimento 2-opt, foi criada uma função chamada flip(início,fim), que pega todos os vértices entre início e fim e inverte a seqüência. Por exemplo, ao chamarmos flip(4,8), teríamos:
ANTES: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 13 15
APÓS: 0 1 2 3 4 10 9 8 7 6 5 11 12 13 14 15
O algoritmo de melhoria 2-opt é o algoritmo 4 a seguir.
Durante a implementação do algoritmo 2-opt, um ''bug'' na implementação permitiu a visualização de uma nova melhoria. Inicialmente, o algoritmo 2-opt não funcionou. Após sua execução, nenhuma melhoria ocorria. Para testar e encontrar o problema, um flip aleatório foi causado no ciclo antes de submetê-lo ao 2-opt. Se o algoritmo estivesse funcionando, ele deveria desfazer a inversão. Ele não desfez, porque havia um bug. Após ter sanado o problema, a surpresa foi que ele também não desfez a inversão causada antes, mas outras inversões foram feitas, causando um resultado ainda melhor que o ciclo original sem a inversão causada. A idéia que surgiu desse fato foi implementar todas as combinações de inversões antes de acionar o algoritmo 2-opt. O resultado foi excelente. Na primeira tentativa foi obtido o resultado 25395 para o problema brazil58, que é o melhor resultado já encontrado e talvez possa até ser ótimo.
A segunda heuristica de melhoria criada foi designada de flip + 2opt. e está apresentado no algoritmo 5 a seguir. Posteriormente, constatou-se na literatura que esse algoritmo é o consagrado algoritmo Lin-Kernighan [Rei94]. Uma das principais idéias do algoritmo Lin-Kernighan é fazer modificações complicadas no ciclo, de modo a aumentar o ciclo, para em seguida aplicar a melhoria. Essa técnica permite eliminar os mínimos locais que eventualmente o algorítmo encontrou.
O algoritmo da inserção mais distante possui dois loops, ambos de
tamanho . Portanto esse algoritmo é
. No
programa principal, ele é invocado em um loop de tamanho também,
para varia o vérice inicial e ficar com o melhor resultado. Portanto,
é
.
A função flip() é no pior caso. Devido ao uso de vetores,
é preciso movimentar todos os vértices. Entretanto, no pior caso será
, pois um flip grande tem um flip equivalente menor, complemento
do numero de vértices. Essa função pode ficar 
se for implementado
com outra estrutura de dados.
No procedimento 2opt, a função flip é chamada para cada combinação
de 2 dos N vértices. É portanto
. O loop while
itera um numero muito pequeno em relação a .
O último procedimento ficou com complexidade
,
já que ele executa o procedimento 2opt dentro de dois loops, o externo
de tamanho 
e o interno de tamanho . Dentro temos
três procedimentos: medir o ciclo, 
, fazer o flip, ,
e fazer o 2opt básico,
. A tabela 2 resume
as complexidades dos algoritmos implementados.
|
Como já foi dito, o resultado para o o problema brazil58 se igualou ao resultado publicado na TSPLIB. A execução do algoritmo gerou a seguinte saída, com os resultados parciais do inserção mais distante e 2opt básico. O ciclo impresso é o ciclo final.
58 cities in Brazil (Ferreira)
Ciclo inicial (insercao mais distante): 25664.000000
Apos melhoria 2-opt: 25643.000000
Apos melhoria flip e 2-opt: 25395.000000
Melhor Tour obtido:
34,9,51,50,46,48,42,26,4,22,11,56,23,57,43,17,0,29,12,39,24,8,31,19,52,49,3,7,21,
15,41,37,30,6,10,38,20,35,16,25,18,5,27,13,36,14,33,45,55,44,32,28,2,47,54,53,1,40
Os algoritmos de busca local como o do vizinho mais próximo, inserção mais próxima e inserção mais barata são todos baseados na árvore geradora mínima [LL85]. Entretanto, o algoritmo da inserção mais distante é sempre superior aos anteriores. O motivo é que um excesso de busca local pode prejudicar o resultado da heurística.
Embora na prática esse algoritmo sempre vença dos demais
de busca local, demonstrando uma performance de pior caso de 
o ótimo[LL85], até ha pouco tempo não existia
um estudo de pior caso de performance para ele. Muitos artigos pesquisados não apresentam esse resultado. [LL85] afirma que esse algoritmo parece ser difícil de ser analisado, por não ser baseado na árvore geradora mínima, e que novas técnicas seriam necessárias para fazer essa análise, já que a árvore geradora mínima não serve.
Mais recentemente (9 anos após a publicação de [LL85]), Rozenkrantz provou que a garantia de performance para
qualquer algoritmo de inserção é
. Posteriormente, o artigo [BKP94] melhorou esse resultado,
provando que o pior caso de performance dos algoritmos de inserção é
.
As heurísticas adotadas para a melhoria do ciclo obtido não diminui o pior caso de performance, nem mesmo no caso de heurísticas como a Lin-Kernighan, que está sempre entre as melhores. Um caminho pode conter um excesso de mínimos locais onde a heurística não consegue obter nenhuma melhoria.
Para fazer as comparações e testes, foram testados vários problemas obtidos da TSPLIB. As tabelas 3 e 4 mostram os resultados obtidos pelas heurísticas, com e sem a melhoria, comparando com os melhores resultados obtidos para cada problema e também comparando com o resultado do limite inferior Held-Karp calculados por [Net99].
|
|
Os resultados mostram uma aproximação muito boa para a maioria dos problemas experimentados. O problema pr107 parece ter chegado a uma solução melhor qua a publicada na TSPLIB, mas não foi. A diferença ocorreu por erros de arredondamento. O mesmo pode ter ocorrido no problema pr144. Na própria FAQ da TSPLIB ttem um aviso para não submeter novas soluções antes de avaliar se não é erro de arredondamento. Não foi totalmente comprovado, mas é muito mais provável ser erro de arredondamento.
Os cálculos foram feitos sem arredondamento, exatos, sendo que os publicados estão arredondados. O erro é grande porque o tipo de arquivo de entrada é diferente do brazil58, é composto por coordenadas x e y e o cálculo das distâncias não dá exato. O código desenvolvido pôde ler esse tipo de entrada também devido ao parser que foi implementado. Isso foi feito justamente para poder aumentar o número de entradas que podiam ser usadas.
O resultado puro da heurística da Inserção do mais Distante mostrou que ela é realmente muito boa. O pior resultado
foi de pouco mais de 6% para o problema pr136. Esse resultado bate exatamente com o pior caso de performance de
. Para 
o pior caso é 
. Para 
, o pior caso é de 
. Apesar de depender de , ele não varia muito, devido ao logaritmo.
A heurística 2opt pura parece não melhorar muito o resultado. Parece que a melhoria significativa necessita eliminar mínimos locais, como foi conseguido com a execução de um flip antes de realizar o 2-opt, para cada par de vértices (flip+2opt). O pior resultado do conjunto foi para o problema pr76, com 2.86%. Na média, não chegou a 1%.
|
Resultado:
![\includegraphics[width=0.60\textwidth]{figuras/binpacking.eps}](img11.png)
![\includegraphics[width=0.30\textwidth]{figuras/vertex.eps}](img23.png)
![\includegraphics[%%
width=0.40\textwidth]{figuras/2opt.eps}](img87.png){kind=small}
Trabalho Pr\'{a}tico: 2.
Arquivo (.zip): lucianobertini.tar.gz.
Filename = lucianobertini.tar.gz
Extensao = tar
Descompactando ...
x entrada, 183 bytes, 1 tape blocks x makefile, 188 bytes, 1 tape blocks
x otimo.c, 2333 bytes, 5 tape blocks
Compilando e executando ...
gcc otimo.c -o otimo
./otimo > saida
Aqui est\'{a} o arquivo de saida:
0
2
1
5
3
4
6
O resultado est\'{a} correto.
------------------------------------------------------------------------
O software implementado é bastante estável quanto à leitura da entrada TSPLIB. Foi implementado um parser capaz de interpretar dois tipos de arquivos: Matrix (igual ao brazil58) e o mais usado de todos, o EUC_2D, que é composto pelas coordenadas cartesianas de cada ponto. O código ficou simples o bastante para se optar por não criar arquivos separados e makefile.
Somente dois arquivos foram anexados, contendo toda a implementação realizada no trabalho. O arquivo otimo.c tem a implementação da solução ótima. O programa otimo também tem o parser, porem ele foi reduzido para simplificar, já que não há interesse em executálo para algum outro problema se não a matriz dada.
O arquivo mdist.c traz todas as funções usadas na implementação das heurísticas.
/*
* Arquivo mdist.c
* Implementa heuristicas da insercao mais distante e 2opt para a
* solucao do Problema do Caixeiro Viajante (TSP), alem de uma
* melhoria denominada flip+2opt
* Interpreta corretamente dois tipos de arquivos da TSPLIB:
* UPPER_ROW e EUC_2D
*
* Compilar com:
* gcc -Wall -lm mdist.c -o mdist
*
* Luciano Bertini 15/Jun/2003
*
* Qualquer questao sobre este codigo, contate
* bertini@dcc.ufmg.br
* */
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>
#define INF 1E+100
/* Obtem o indice anterior e proximo de um vetor circular
* de tamanho N */
#define prev(a) ((a==0)?N-1:a-1)
#define next(a) ((a==(N-1))?0:a+1)
/* Estrutura para representar uma cidade pelas coordenadas
* usada no tipo de arquivo EUC_2D antes de calcular as distancias */
struct ponto{
double x;
double y;
};
double **g; /*matriz representante do grafo de entrada */
int N; /*Numero de cidades*/
/* Mede o tamanho de um ciclo de n arestas
* considera a aresta (n-1,0)
* Retorna o tamanho do ciclo */
double medeciclo(int *t, int n)
{
int i;
double l=0;
for(i=0;i<n-1;i++)
l=l+g[t[i]][t[i+1]];
l=l+g[t[n-1]][t[0]];
return l;
}
/* Verifica se um ciclo eh Hamiltoniano */
void verifica_ciclo(int *t)
{
int *v;
int i;
v=(int*)malloc(N*sizeof(int));
for(i=0;i<N;i++)
v[i]=0;
for(i=0;i<N;i++)
v[t[i]]++;
for(i=0;i<N;i++)
if(v[i]!=1){
printf("Erro, o caminho nao e hamiltoniano(%d).\n",v[i]);
free(v);
return;
}
free(v);
}
/* Heuristica para determinar uma solucao para o problema do caixeiro viajante (TSP)
* atraves da insercao do vertice mais distante. Inicia-se com um ciclo de uma unica aresta
* e vai inserindo cada vertice mais distante que qualquer vertice do ciclo. A escolha do ponto
* de insercao dentro do ciclo eh feita de modo a minimizar o custo final do ciclo*/
void insdist(int s, int *ciclo)
{
int i, j, k1, k2, l, min, max, melhor;
int m=1;
char *inserido;
inserido=(char*)malloc(N);
for(i=0;i<N;i++)
inserido[i]=0;
inserido[s]=1;
ciclo[0]=s;
for(m=1;m!=N;m++)
{
/* Encontra o vertice k2 mais distante do que
* qualquer vertice do ciclo */
max=0;
for(i=0;i<N;i++)
{
if(inserido[i]) continue;
/* Encontra o vertice k1 do ciclo que esta mais
* proximo do vertice i */
min=1000000; /*infinito*/
for(j=0;j<m;j++)
if((l=g[i][ciclo[j]])<min){
min=l;
k1=ciclo[j];
}
/* Seleciona k2 baseado na distancia de i ate k1 */
if((l=g[i][k1])>max){
max=l;
k2=i;
}
}
inserido[k2]=1;
/* Procura pela melhor aresta (i,i+1) (menor custo) do ciclo para inserir k2*/
min=1000000; /*infinito*/
for(i=0;i<m;i++){
if((l=g[ciclo[i]][k2]+g[k2][ciclo[(i+1)%m]]-g[ciclo[i]][ciclo[(i+1)%m]])<min){
min=l;
melhor=i+1; /* "melhor" sera a posicao onde ficara k2 no novo ciclo */
}
}
/* Insere k2 na posicao melhor */
for(j=m-1;j>=melhor;j--)
ciclo[j+1]=ciclo[j];
ciclo[melhor]=k2;
}
free(inserido);
}
/* Imprime um vetor desde o indice i ate o indice f */
void printvetor(int *v, int i, int f)
{
int k;
printf("{");
for(k=i;k<f;k++)
printf("%d,",v[k]);
printf("%d}\n",v[k]);
}
/* Um flip eh uma alteracao no vetor que pega a sequencia de vertices
* do ciclo de inicio ate fim e inverte de posicao. Exemplo:
* ANTES:
* 0 1 2 3 4 5 6 7 8 9 10 11 12 13 13 15
* APOS flip com inicio=5 e fim=10:
* 0 1 2 3 4 10 9 8 7 6 5 11 12 13 14 15
* Equivale a um "2opt move" */
void flip(int inicio, int fim, int n, int *v)
{
int tam, i, p1, p2, aux;
if(inicio>fim)
tam=n-inicio+fim+1;
else
tam=fim-inicio+1;
p1=inicio;
p2=fim;
for(i=0;i<tam/2;i++){
aux=v[p1];
v[p1]=v[p2];
v[p2]=aux;
p1=(p1==n-1)?0:p1+1;
p2=(p2==0)?n-1:p2-1;
}
}
/* Tenta melhorar o ciclo efetuando cada possivel alteracao
* no ciclo atraves de um flip */
void dois_opt(int *ciclo)
{
int k, ia, a, b, pa, nb, ib, fim=0;
while(!fim){
fim=1;
for(k=1;k<=(N%2+N/2);k++)
for(ia=0;ia<N;ia++){
ib=(ia+k)%N;
a=ciclo[ia];
b=ciclo[ib];
pa=ciclo[prev(ia)];
nb=ciclo[next(ib)];
if((g[pa][b]+g[a][nb])<(g[pa][a]+g[b][nb]))
{
flip(ia, ib, N, ciclo);
fim=0;
}
}
}
}
/* Executa novamente a heuristica 2opt mas fazendo antes um flip no ciclo, mesmo
* que esse flip aumente o tamanho do ciclo. Experimenta todas as poss´iveis combinacoes de flips */
double flip_dois_opt(int *ciclo, int *melhor_ciclo)
{
double min,l;
int i,j,k;
int *old;
min=INF;
old=(int*)malloc(N*sizeof(int));
for(i=1;i<=(N%2+N/2);i++){
for(j=0;j<N;j++){
for(k=0;k<N;k++) old[k]=ciclo[k];
flip(j,(j+i)%N,N,ciclo);
dois_opt(ciclo);
l=medeciclo(ciclo,N);
if(l<min){
min=l;
for(k=0;k<N;k++) melhor_ciclo[k]=ciclo[k];
}
else
for(k=0;k<N;k++) ciclo[k]=old[k];
}
}
free(old);
return min;
}
/* Main: Recebe da linha de comando o nome do arquivo de entrada */
int main(int argc, char **argv)
{
FILE *fd;
char buf[20];
char comment[50];
char ewformat[20];
char ewtype[20];
struct ponto *P;
int i, j, k;
double aux;
int *ciclo; /* caminho encontrado */
int *melhor_ciclo1; /* melhor ciclo obtido com a insercao mais distante */
int *melhor_ciclo2; /* melhor ciclo obtido com 2opt */
int *melhor_ciclo3; /* melhor ciclo obtido com flip + 2opt */
double l; /* comprimento do ciclo */
double min;
/* Testa os argumentos da linha de comando */
if(argc!=2){
printf("Uso: %s <arquivo TSP>\n", argv[0]);
exit(0);
}
/* Parser do arquivo de entrada.
* Interpreta dois tipos de arquivo: EXPLICIT/UPPER_ROW e arquivo de coordenadas euclideanas EUC_2D
* Considera invalido se o arquivo nao iniciar com a palavra NAME */
fd=fopen(argv[1],"r");
fscanf(fd,"%s",buf);
if(strcmp(buf,"NAME")!=0&&strcmp(buf,"NAME:")!=0){
printf("%s: O arquivo de entrada nao eh um arquivo TSP valido\n", argv[0]);
exit(0);
}
/* Parser
* O laco while termina quando acabar de ler o cabecalho */
while(1)
{
fscanf(fd,"%s",buf);
if(strcmp(buf,"COMMENT:")==0)
fgets(comment, 50, fd);
else if(strcmp(buf,"DIMENSION:")==0){
fscanf(fd," %d",&N);
}else if(strcmp(buf,"COMMENT")==0){
fscanf(fd," : ");
fgets(comment, 50, fd);
}
else if(strcmp(buf,"DIMENSION")==0){
fscanf(fd," : %d",&N);
}
else if(strcmp(buf,"EDGE_WEIGHT_FORMAT:")==0){
fscanf(fd," %s",ewformat);
}
else if(strcmp(buf,"EDGE_WEIGHT_FORMAT")==0){
fscanf(fd," : %s",ewformat);
}
else if(strcmp(buf,"EDGE_WEIGHT_TYPE:")==0){
fscanf(fd," %s",ewtype);
}
else if(strcmp(buf,"EDGE_WEIGHT_TYPE")==0){
fscanf(fd," : %s",ewtype);
}
else if(strcmp(buf,"EDGE_WEIGHT_SECTION")==0)
break;
else if(strcmp(buf,"NODE_COORD_SECTION")==0)
break;
else if(strcmp(buf,"EOF")==0){
printf("%s: Erro no reconhecimento do arquivo\n", argv[0]);
printf("%s: O campo EDGE_WEIGHT_FORMAT ou NODE_COORD_SECTION nao existe\n", argv[0]);
exit(0);
}
}
/* Nao aceita arquivos que nao sao nem de coordenadas euclideanas EUC_2D e nem
* matriz diagonal superior UPPER_ROW. Tambem nao aceita o arquivo se for UPPER_ROW
* mas nao for tipo EXPLICIT */
if((strcmp(ewformat,"UPPER_ROW")==0&&strcmp(ewtype,"EXPLICIT")!=0)||
(strcmp(ewformat,"UPPER_ROW")!=0&&strcmp(ewtype,"EUC_2D"))!=0){
printf("%s: Arquivo TSP nao suportado\n", argv[0]);
printf("%s: O arquivo deve ser do tipo matriz UPPER_ROW tipo EXPLICIT \n",argv[0]);
printf("%s: Ou de coordenadas euclideanas EUC_2D\n", argv[0]);
exit(0);
}
/* Imprime a linha de comentario extraida do arquivo de entrada
* A expressao simbolica serve para eliminar um espaco em branco deixado pelo parser no inicio */
printf("\n%s",(comment[0]==' ')?comment+1:comment);
/* Aloca memoria para os vetores e matrizes */
ciclo=(int*)malloc(N*sizeof(int));
melhor_ciclo1=(int*)malloc(N*sizeof(int));
melhor_ciclo2=(int*)malloc(N*sizeof(int));
melhor_ciclo3=(int*)malloc(N*sizeof(int));
g=(double**)malloc(sizeof(double*) * N);
for(i=0;i<N;i++)
g[i]=(double*)malloc(sizeof(double) * N);
if(strcmp(ewformat,"UPPER_ROW")==0){
/* Arquivo de entrada tipo UPPER_ROW
* obtem as distancias diretamente */
for(i=0;i<N;i++){
g[i][i]=0;
for(j=i+1;j<N;j++){
fscanf(fd,"%lf",&aux);
g[i][j]=g[j][i]=aux;
}
}
}else{
/* Arquivo de entrada tipo EUC_2D
* Calcula as distancias entre os pontos, sem arredondamento */
P=(struct ponto*)malloc(N*sizeof(struct ponto));
for(i=0;i<N;i++)
fscanf(fd,"%lf %lf %lf\n",&aux,&(P[i].x),&(P[i].y));
for(i=0;i<N;i++)
for(j=0;j<N;j++){
g[i][j]=(sqrt((P[i].x-P[j].x)*(P[i].x-P[j].x)+(P[i].y-P[j].y)*(P[i].y-P[j].y)));
}
}
/* executa o algoritmo da insercao do vertice mais distante N vezes,
* uma vez para cada possivel vertice inicial, obtendo o melhor ciclo*/
min=INF;
for(i=0;i<N;i++){
insdist(i,ciclo);
l=medeciclo(ciclo,N);
if(l<min){
min=l;
for(k=0;k<N;k++) melhor_ciclo1[k]=ciclo[k];
}
/* Verifica se o ciclo gerado eh um ciclo hamiltoniano */
verifica_ciclo(ciclo);
}
/* restaura o ciclo atual com o melhor ciclo obtido */
for(k=0;k<N;k++) ciclo[k]=melhor_ciclo1[k];
printf("\nCiclo inicial (insercao mais distante): %f\n",min);
/* executa a heuristica de melhoria 2-opt sobre o melhor
* ciclo obtido com a insercao do vertice mais distante */
dois_opt(ciclo);
/* copia o ciclo obtido */
for(k=0;k<N;k++) melhor_ciclo2[k]=ciclo[k];
/* Mede e imprime o comprimento do ciclo obtido */
l=medeciclo(melhor_ciclo2,N);
printf("Apos melhoria 2-opt: %f\n",l);
/* Melhora o ciclo obtido atraves da heuristica flip + 2opt
* que consiste em executar 2opt ciclicamente executando-se antes
* cada possivel flip no vetor */
l=flip_dois_opt(ciclo, melhor_ciclo3);
printf("Apos melhoria flip e 2-opt: %f\n",l);
/* Imprime o melhor ciclo obtido */
printf("\nMelhor Tour obtido:\n");
printvetor(melhor_ciclo3,0,N-1);
/* Fim */
printf("\n");
return 0;
}
/* Arquivo otimo.c
*
* Encontra a solucao otima para o Problema do
* Caixeiro Viajante, baseado no algoritmo de
* busca em profundidade Depth-First-Search (DFS).
*
* Le o arquivo de nome "entrada"
* e gera a saida na saida padrao.
*
* Luciano Bertini
* Projeto e Analise de Algoritmos
* 15/06/2003
* */
#include <stdio.h>
int N; /* numero de vertices */
int *ciclo; /* ciclo atual */
int *melhor_ciclo; /* melhor ciclo encontrado */
int *explorado; /* vetor para armazenar se o vertice foi explorado pelo DFS*/
int **g; /* matriz de distancias */
int nivel=0; /* profundidade alcancada pelo DFS*/
int min=10000; /* usado para selecionar o menor ciclo */
int medeciclo(int *t)
{
int i;
int l=0;
for(i=0;i<N-1;i++)
l=l+g[t[i]][t[i+1]];
l=l+g[t[N-1]][t[0]];
return l;
}
/* Esta funcao implementa o algoritmo DFS modificado para
* poder percorrer todos os caminhos possiveis. Apos o retorno, o vertice
* eh desmarcado como explorado, permitindo que ele seja explorado novamente */
void dfs(int v, int nivel)
{
int i,j,dist;
explorado[v]=1;
ciclo[nivel]=v;
if(nivel==N-1){
/* completou um ciclo */
dist=medeciclo(ciclo);
if(dist<min){
min=dist;
for(j=0;j<N;j++)
melhor_ciclo[j]=ciclo[j];
}
}
for(i=0;i<N;i++){
if(!explorado[i]){
dfs(i,nivel+1);
explorado[i]=0;
}
}
}
int main()
{
int i,j;
FILE *fd;
char buf[20];
/* Parser do arquivo de entrada.*/
fd=fopen("./entrada","r");
do{
fscanf(fd,"%s",buf);
if(strcmp(buf,"DIMENSION:")==0)
fscanf(fd," %d",&N);
else if(strcmp(buf,"DIMENSION")==0)
fscanf(fd," : %d",&N);
}while(strcmp(buf,"EDGE_WEIGHT_SECTION")!=0);
/* Aloca memoria para os vetores e matrizes */
ciclo=(int*)malloc(N*sizeof(int));
explorado=(int*)malloc(N*sizeof(int));
melhor_ciclo=(int*)malloc(N*sizeof(int));
g=(int**)malloc(N*sizeof(int*));
for(i=0;i<N;i++)
g[i]=(int*)malloc(N*sizeof(int));
/* Leitura da matriz g */
for(i=0;i<N;i++){
g[i][i]=0;
for(j=i+1;j<N;j++){
fscanf(fd,"%d",&g[i][j]);
g[j][i]=g[i][j];
}
}
for(i=0;i<N;i++)
explorado[i]=0;
dfs(0,0);
/* Resultado */
for(i=0;i<N;i++)
printf("%d\n",melhor_ciclo[i]);
return 0;
}
This document was generated using the LaTeX2HTML translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -show_section_numbers main.tex
The translation was initiated by Luciano Bertini on 2003-06-21