Universidade
Federal de Minas Gerais - UFMG
Instituto
de Ciências Exatas - ICEx
Departamento
de Ciência da Computação
Disciplina:
Projeto e Análise de Algoritmos
Professor:
Nivio Ziviani
Aluna:
Cristiana Maria Nascimento Gomes
Trabalho Prático 3
O objetivo deste trabalho é projetar
e implementar um sistema de programas para recuperar ocorrências de padrões em
arquivos constituídos de documentos, utilizando algoritmos lineares de busca
seqüencial.
O sistema de programas recebe do
usuário uma cadeia de caracteres (padrão), se a busca é exata (k=0) ou
aproximada (0 < k < m), e imprime todas as ocorrências do padrão no
texto. Foram utilizados os seguintes algoritmos:
Algoritmo
de Boyer-Moore-Horspool (BMH) e Baetas (Shift-And) para casamento exato de
padrões.
Algoritmo
proposto por Wu e Manber (extensão do Shift-And) para casamento aproximado de
padrões.
P
= vetor que contém os caracteres do padrão
Pi
= posiçao i de P
m
= tamanho do padrão
T
= texto no qual se procura o padrão
k
= número de erros admissíveis
Para os teste realizados deste
trabalho foram utilizados os arquivos de documentos da coleção TREC disponível
em export/texto2/wsj, com as seguintes características:
Coleção Tamanho (Mb)
wsj88 109
wsj88_10 10
wsj88_20 20
wsj89 2.8
1.
Explicação detalhada dos algoritmos e estruturas de dados utilizados para
resolver o problema
Algoritmo de Boyer-Moore-Horspool (BMH)
O algoritmo de BMH é uma
simplificação do algoritmo de Boyer-Moore (BM). O BM trabalha com duas
heurísticas: match heuristic e a ocurrence heuristic, e funciona da seguinte
maneira: posiciona o padrão sobre o caracter mais a esquerda do texto e tenta
casar da direita para esquerda. Se nenhum erro ocorre, então o padrão foi
encontrado. Caso contrário o algoritmo calcula um deslocamento de forma que o
padrão é movido para uma posição a direita antes que seja possível existir um
casamento exato.
O BM tem uma versão simplificada SBM
que usa somente a ocurrence heuristic. Essa heurística é utilizada para o
cálculo do deslocamento. Quando um erro ocorre a ocurrence heuristic usa a
informação sobre onde o bad character (caractere que causou o erro) do texto
ocorre no padrão para propor um novo deslocamento (d). A principal
justificativa para esta versão é que, na prática, padrões não são periódicos.
BMH foi apresentado por Horspool, que notou que qualquer caractere do texto
pode ser usado para endereçar a tabela de ocorrências (d). Baseado nisto, usou
o algoritmo SBM e endereça a tabela d
com o caractere no texto correspondente ao último caractere do padrão.
Para evitar comparação quando o valor na tabela é zero (último caractere do
padrão), foi atribuído o valor m (tamanho do padrão) para entrada na tabela de
ocorrências para o último caractere no padrão. Portanto, a tabela de ocorrências
é somente calculada para os m-1 caracteres do padrão. Então temos,
d[x] = min {s | s = m
(1<=s<m e padrão [m-s] = x)}
e
qualquer caractere que não pertence ao padrão receberá valor m.
Perceba que d só depende do padrão,
ou seja, pode ser pré-calculado antes de se realizar a busca.
Exemplo
Alfabeto (a) = A C G T
Tabela de ocorrências: d[A] = 4
d[C]
= 3
d[G]
= 1
d[T]
= 2
Tentativa 1
Texto: T A T G [C] A C T G A
Padrão: A C T G [A]
Delocamento de d[C] = 3
Tentativa 2
Texto: T A T G C A C [T] G A
Padrão: A C T G [A]
Delocamento de d[T] = 2
Tentativa 3
Texto: T A T G C A C T G [A]
Padrão: A C T G [A] MATCH
Observe que esse algoritmo é pouco eficiente para alfabetos muito
pequenos se comparado ao tamanho do padrão, porque o deslocamento será muito
pequeno.
Algoritmo Wu e Manber (WM)
O algoritmo de WM permite uma busca
aproximada, ou seja, admite a existência de erros (k) no padrão encontrado no
texto. A medida mais comum de aproximação (palavra do texto e padrão) é
conhecida como distância de edição. Uma palavra P está a uma distância k da
palavra Q se podemos transformar P em Q com uma sequência de inserções de
simples caracteres em (lugares arbitrários) P, deleções de caracteres simples
em P ou substituições de caracteres. O algoritmo de WM funciona da seguinte
forma:
Casamento
Exato-
Considere
R um vetor de bits de tamanho m (tamanho do padrão).
Considere
Rj o valor do vetor R depois do processamento do caractere j do texto. Portanto
este vetor terá informações sobre todos os matches dos prefixos de P que
finalizam na posição j. Mais precisamente, Rj[i] = 1 se os primeiros i
caracteres do padrão casam exatamente os últimos i caracteres até a posição j no
texto, ou seja, P1P2...i = Tj-i+1 + Tj-i+2 ... Tj.
Para cada i com Rj[i] = 1, temos que
checar se Tj+1 é igual a Pi+1. Se Rj[i] = 0, então não existe casamento até i e
portanto não teremos casamento até i+1. Se Tj+1 = P1 então Rj+1[1] = 1. Se
Rj+1[m] = 1 então temos um casamento completo iniciando em (j+1)-m +1 = j-m+2.
A transição de Rj para Rj+1 pode ser calculada rapidamente pelo algoritmo de
Baeza-Yates and Gonnet. O algoritmo é o seguinte, considere o alfabeto S1,
S2,... Sc, para cada caractere Si do alfabeto, pertencente ao padrão, é
construído um vetor S de bits de tamanho m sendo que Si[r] = 1 se Pr = Si. É
fácil verificar que a transição de Rj para Rj+1 executa não mais que um
deslocamento para direita de Rj e uma operação AND com Si, onde Si = Tj+1.
Portanto cada execução pode ser executada com somente três simples operações
aritméticas (três porque estamos usando C e seu deslocamento não preenche os
espaços com um, característica necessária para este algoritmo, e precisaremos
efetuar uma operação OR com uma máscara de 1s). Observe o exemplo na tabela 1
abaixo, onde o padrão é aabac e o texto é aabaacaabacab. A tabela 2 mostra as
máscaras para a, b e c.
Rj Si
P a a b a a c a a b a c a b a b c
a 1 1 0 1 1 0 1 1 0 1 0 1 0 1 0 0
a 0 1 0 0 1 0 0 1 0 0 0 0 0 1 0 0
b 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0
a 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0
c 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 1
Tabela 1 Tabela
2
Casamento Aproximado-
Aqui é possível considerar a existência de erros. Os erros podem ser dos
tipos: inserção, deleção ou substituição.
Considere um outro vetor R1j, que indica todos os possíveis casamentos
até Tj com no máximo 1 inserção, ou
seja, R1j[i] = 1 se os primeiros i caracteres do padrão casam com i dos últimos
i+1 caracteres, até j, do texto. Temos então R[m]=R0[m] = 1 indicando que
existe um casamento exato e R1j [m] = 1 indicando que existe um casamento com
no máximo uma inserção.
A transição de R0 é realizada da mesma maneira que mostrada
anteriormente para casamento exato. Precisamos só definir como será a transição
de R1j para R1j+1. Vamos considerar o caso genérico com k erros, então teremos
k adicionais vetores R (R1, R2, ... Rk). Onde Rd armazena todos os possíveis
casamentos com até d erros. Precisamos definir como seria a transição de Rdj
para Rdj+1. Existem quatro possibilidades de se obter um casamento dos i
primeiros caracteres com erro <=d até Tj+1:
-
Existe um casamento dos primeiros i-1 caracteres com erro <= d até Tj e Tj+1
= Pi. Este caso corresponde ao casamento Tj+1.
-
Existe um casamento dos primeiros i-1 caracteres com erro <= d-1
até Tj. Este caso corresponde a uma
substituição de Tj+1.
-
Existe um casamento dos primeiros i-1 caracteres com erro <= d-1 até Tj+1. Este
caso corresponde a uma deleção de Pi.
-
Existe um casamento dos primeiros i caracteres com erro <= d-1 até Tj. Este
caso corresponde a uma inserção de Tj+1.
Assuma
Tj+1=Si. Teremos a seguinte expressão para Rdj+1:
Rd0
= 111...10...000 (d elementos 1s)
Rdj+1 =
Rshift[Rdj] AND Si OR
Rshift[Rd-1j] OR
Rshift[Rd-1j+1] OR Rd-1j
= Rshift[Rdj] AND Si OR
Rshift[Rd-1j OR Rd-1j+1] OR
Rd-1j.
Temos
2 deslocamentos, 1 AND e 3 ORs para cada Rd.
Toda busca pode ser modelada usando autômatos. Toda essa teoria
anteriormente mostrada usando registradores Rs pode ser melhor visualizada
abaixo.
A
fórmula para qualquer erro mostrada acima pode ser mapeada para o seguinte
formato:
(quando
d=1)
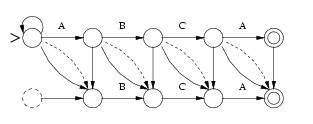
(quando
d=2)
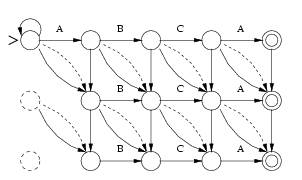
...
Ilustraremos
abaixo um percurso até um casamento com o erro=1 e padrão=ABCA :
Erro=Inserção
MATCH
= ABXCA
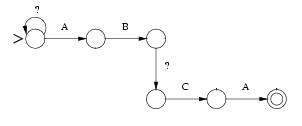
Erro=Substituição
MATCH
= ABXA
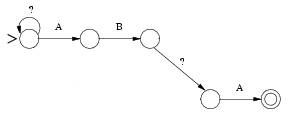
Erro=Remoção
MATCH
= BCA
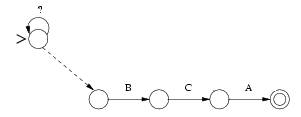
Exemplo
de busca aproximada permitindo 1 erro (remoção):
Padrão
= TEXT
Texto
= EXTEXT
Mácaras
à
M[T] = 1001
M[E] = 0100
M[X] = 0010
Fómulaà Roj+1 = (R0j>>1
& M[T[i]])
Texto R0j>>1 Roj+1 R0j+1>>1 R1>>1 R1j+1
0000 1000
E 1000 0000 1000 1100 1100
X 1000 0000 1000 1110 1010
![]() T 1000 1000 1100 1101 110[1]ext
T 1000 1000 1100 1101 110[1]ext
E 1100 0100 1010 1110 1110
![]() X 1010 0010 1001 1111 101[1]tex
X 1010 0010 1001 1111 101[1]tex
![]()
![]() T 1001 100[1]text 1100 1101 110[1]ext
T 1001 100[1]text 1100 1101 110[1]ext
Casamento Casamentos
Exato com
erro
As colunas onde estão sendo mostrados os casamentos são exatamente a
representação binária do acionamento dos estados de um autômato. Por isso
quando temos o último bit igual a 1 é sinal de que alcançamos o estado final de
um autômato, ou seja, já passamos por todos os estados anteriores admitindo k
erros. Isto significa um casamento.
2.
Análise de complexidade dos principais algoritmos implementados
Foi considerada somente as partes obviamente mais pesadas (que levam
mais tempo de processamento) do programa. Foi considerada como O(1) qualquer
instrução de atribuição ou semelhante. n é o tamanho do texto, m é do padrão e
c do alfabeto. A listagem completa dos algoritmos implementados em C e Pascal
encontra-se no Anexo1.
Boyer-Moore-Horspool
(BMH)
Linguagem C
long
bmh( pd, tx, n )
/* (numero de casamentos) bmh (padrao, linha do
texto, tamanho da linha) */
char
*pd, *tx;
int n;
{
int i,
j, k, m, d[MAX_ALPHABET_SIZE]; /* tabela de ocorrencias */
long
match; /* numero de casamentos */
1 m = strlen(pd);
if( m==0 ) return(1);
2 for( k=0; k<MAX_ALPHABET_SIZE; k++ )
d[k]
= m; /* iniciando tabela de ocorrencias com m */
3
for( k=0; k<m-1; k++ ) d[pd[k]] = m-k-1; /* atribuindo deslocamento adequado para os caracteres do
padrao*/
5
for( k=m-1; k < n; k += d[tx[k] & (MAX_ALPHABET_SIZE-1)] ) { /*
efetua o deslocamento */
4 for( j=m-1, i=k; j>=0
&& tx[i] == pd[j]; j-- ) i--;
/* checando casamento */
if( j == (-1) ) /*se houve
casamento*/
if(opc==5){
printf("MATCH posicao
%d\n",k-m+1);
match++;
}else{
return(1);
/* retorna 1 quando encontra o primeiro casamento */
}
5. }
return(match); /* retorna o numero de casamentos ocorridos nesta linha
do texto */
}
Bloco
1: Executa m = strlen(pd). A função strlen foi considerada como sendo O(tamanho
de pd), neste caso, O(m).
Bloco
2: Executa uma atribuição (d[k]=m, O(1)) c vezes, sendo O(c) (c=tamanho do
alfabeto).
Bloco
3: Executa uma atribuição (d[pd[k]]=m-k-1, O(1)) m-1 vezes, sendo O(m-1).
Bloco
4: Executa uma atribuição e uma comparação (O(1) cada) m vezes no pior caso,
sendo O(m).
Bloco
5: Executa n-m vezes no pior caso, sendo O(n-m). E mais o bloco 4, sendo
O(n-m).O(m) = O(n.m - m**2).
____________________________________________________
O(c)
+ O(m) + O(n.m - m**2) = O(n.m)
Pior
caso: O(nm) (tempo de execução do algoritmo de força bruta)
O pior caso no algoritmo BMH
acontece quando temos um erro somente na m-ésima comparação e caractere do bad
caracter implica num deslocamento de 1. Se esse caso se repete durante todo o
texto então o algoritmo irá realizar:
![]() n+(n-1)+(n-2)+...+(n-(m-1))
n+(n-1)+(n-2)+...+(n-(m-1))
=
n.m - (1+2+...(m-1)) = n.m - ((m).(m-1)/2) = n.m - m**2/2 + m/2
Exemplo:
G será sempre o bad caracter causando um deslocamento de 1 (d[G]=1).
Texto: G G G G G G G G G G G G
Padrão: . . . . . . . . . C G G
Melhor
caso: O(n/m)
O melhor caso ocorre quando o erro
ocorre na primeira comparação e o bad character não existe no padrão. Neste
caso incrementa-se o deslocamento d de m. Se o melhor caso ocorre
repetidamente, o algoritmo examina somente uma fração de 1/m dos caracteres do
texto.
Caso
Médio:
O(
n/m ) p/ c muito grande, e
n
( 1/m + 1/2c ) p/ (c<<n),
onde
c = tamanho do alfabeto.
Algoritmo Wu e Manber (WM)
Linguagem
C
//pré-procecssamento
void
preproc(char *p, long k) {
int i, j, m; /* pattern size */
1 m = strlen(p);
2 for (i = 0; i < (k + 1); i++) {
Start[i] = 0; /* zerando a mascara
de inicializacao dos Rs */
for
(j = 0; j <= i; j++) {
Start[i] |= 1 << (m - j); /*
construindo os automatos de forma a permitir um numero de erros <=k*/
}
2.}
3
for (i = 0; i < ALPHABET_SIZE; i++) {
S[i] = 0; /* zerando a mascara de
caracteres do alfabeto */
valid[i] = ((i >= 'a')
&& (i <= 'z')) || ((i >= 'A') && (i <= 'Z'));
/* registrando os
caracteres que fazem parte do alfabeto usado*/
3. }
M = 0;
4 for (i = 0; i < m; i++) { /* inicializa mascaras de caracteres
do alfabeto */
if (((p[i] >= 'a')
&& (p[i] <= 'z')) || ((p[i] >= 'A') && (p[i] <= 'Z')))
{
/* se o caractere do
padrao faz parte do alfabeto usado */
S[p[i]] |= 1 << (m - 1 - i); /* marca com 1 todas as ocorrencias de p[i]
no padrao */
M
|= 1 << (m - 1 - i); /*
marca com 1 todas as posições dos caracteres do padrao para busca exata*/
}
else
{
S['
'] |= 1 << (m - 1 - i); /* S
contem 1 em todas as posições cujo caracter nao faz parte do alfabeto*/
}
4.}
5 for (i = 0; i < ALPHABET_SIZE; i++) {
if (!valid[i]) {
S[i] = S[' ']; /* caso
i nao faz parte do alfabeto recebe a mascara constuida em S[' '] */
}
5.}
}
Bloco
1: Executa m = strlen(p). A função strlen foi considerada como sendo O(tamanho
de P), neste caso, O(m).
Bloco
2: Executa S[i:0..k]S[j:0..i] O(1) = S[i:0..k](i+1) = S[j:0..k]i+
S[j:0..k]1=k+(k(k+1)/2)=k**2/2 + 3k/2. Sendo O(k**2).
Bloco
3: O(c) (c= tamanho do alfabeto)
Bloco
4: O(m)
Bloco
5: O(c)
____________________________________________________
O(c)+O(m)+O(k**2) = O(c) (para c grande em relação a m)
Observe que se k é grande de maneira que k**2 ultrapasse c e m, teríamos
O(k**2). Isso normalmente não acontece para padrões de tamanho pequeno, onde um
número de erros muito grande tornaria a consulta por um padrão quase
indefinido. Outro caso poderia ser O(m), se o padrão é maior que c e maior que
k**2. Por exemplo, a busca de uma cadeia de m=100 caracteres que representa um
gene (c=4) pode tranqüilamente admitir 7 erros (k**2=49), sem perder a
qualidade da resposta. Mas, na maioria dos casos, é O(c) para a fase de
pré-processamento.
//pesquisa
long
Wu_Manber(char *p, char *t, long k) {
long i,
j,
m, /*
tamanho do padrao */
n, /*
tamanho da sequencia */
matchfound, /* diz
se um casamento foi encontrado */
R0[MAX_NUMBER_OF_ERRORS], /* mascaras de estado anterior */
R1[MAX_NUMBER_OF_ERRORS]; /* mascaras de estado atual */
char
newt[MAX_MODIFIED_LINE_SIZE]; /* sequencia entre espacos */
long
count; /*
registra a quantidade de matches ocorridos */
strcpy(newt, " ");
1
strcat(newt, t);
strcat(newt, " ");
2
n = strlen(newt);
3
m = strlen(p);
matchfound = FALSE;
4 for (i = 0; i <= k; i++) { /* inicializa
mascaras de estado */
R1[i] = Start[i];
R0[i] = Start[i];
}
count=0;
7 for (i = 0; i < n; i++) { /* executa o
algoritmo */
R1[0]
= ((R0[0] >> 1) & S[newt[i]]) | (Start[0] & R0[0]);
/*checando casamento inteiro */
5 for
(j = 1; j <= k; j++) {
/*checando casamento com erro */
R1[j] = ((R0[j] >> 1) & S[newt[i]]) |
((R0[j-1] | ((R1[j-1] | R0[j-1]) >> 1)) & M) | (Start[0] &
R0[j]);
}
6 for (j
= 0; j <= k; j++) { /* atribui estado atual no anterior */
R0[j] = R1[j];
if
(R1[j] & 1) { /* se bit menos significativo estiver ativo, entao
tem-se um casamento na linha atual do
texto */
matchfound = TRUE;
count+=1;
}
}
}
return count;
7.}
Bloco
1: O(n) (n=tamanho do texto)
Bloco
2: O(n)
Bloco
3: O(m)
Bloco
4: O(k+1)
Bloco
5: O(k)
Bloco
6: O(k+1)
Bloco
7: O(n)*(O(k)+O(k+1))=O(n.(k+1))
____________________________________________________
O(m)+O(n.(k+1))
= O(n.k) (pior caso)
Implementações
atuais deste algoritmo executa em O(n) para padrões considerados pequenos.
Obs.:
As ordens apresentadas acima é uma junção de todas as instruções do bloco, que
normalmente são O(1).
A seguir a análise do mesmo
algoritmo na linguagem Pascal (código atualizado – Anexo1).
Algoritmo Wu e Manber (WM)
Linguagem Pascal
procedure shiftAndPreprocess;
var j, bit, a:
integer;
begin
1 m :=
length(p);
2 for
j:=ord('a') to ord('z') do
Masc[j] := 0;
3 for
j:=ord('A') to ord('Z') do
Masc[j] := 0;
bit :=
1;
4 for
j:=1 to m do begin
a
:= ord(p[j]);
Masc[a] := Masc[a] or bit;
bit
:= bit shl 1;
end;
end;
Bloco
1: O(m)
Bloco
2: O(c) (c = tamanho do alfabeto)
Bloco
3: O(c)
Bloco
4: O(m)
____________________________________________________
O(m)+O(c)
= O(c)
procedure shiftAndSearch;
var
i, j : integer;
R : array[0..m]of
integer;
Rant,
Rnovo, bit , bitaux: integer;
begin
1 for
j:=1 to m do
R[j] := 0;
2 n :=
length(T);
bit :=
0;
bitaux:= 1;
3 for
j:=1 to k do begin
R[j] := bit;
bit := (bit shl 1)or bitaux;
bitaux
:= bitaux or bit;
end;
bit :=
0;
4 for
i:=1 to n do begin
Rant := bit;
Rnovo := ((Rant shl 1) or 1) and Masc[ord(T[i])];
bit
:= Rnovo;
5 for j:=1 to k do begin
6 Rnovo := ((R[j] shl 1) and
Masc[ord(T[i])])or Rant or ((Rant or Rnovo) shl 1);
Rant := R[j];
R[j] := Rnovo;
5. end;
7 if ((Rnovo and lastbit)<>0) then
begin
matchs := matchs + 1;
end;
4. end;
end;
Bloco
1: O(m)
Bloco
2: O(n)
Bloco
3: O(k)
Bloco
4: O(n).(O(Bloco 5).O(Bloco 6)+O(Bloco 7))
Bloco
5: O(k).O(Bloco 6)
Bloco
6: O(x) (não sabemos ao certo como são computadas as operações de shift, or e
and em Pascal, x = ?)
Bloco
7: O(x)
Bloco
4: O(n).(O(k).O(x)+O(x))
____________________________________________________
O(n).O(k.x)
= O(n.k.x) (pior caso)
Tentaremos provar a existência de um x![]() 1 na seção de testes, através da comparação com o algoritmo
em linguagem c. Isso pode ser feito porque temos uma complexidade semelhante e
sabemos que as operações em questão na linguagem c executam em O(1).
1 na seção de testes, através da comparação com o algoritmo
em linguagem c. Isso pode ser feito porque temos uma complexidade semelhante e
sabemos que as operações em questão na linguagem c executam em O(1).
3.
Resultados de experimentos para avaliar empiricamente o desempenho dos
algoritmos
Foram utilizados os arquivos de
documentos da coleção TREC disponível em /export/texto2/wsj da máquina
turmalina.dcc.ufmg.br, com as seguintes características:
Coleção Tamanho (MB)
wsj88 109
wsj88_10 10
wsj88_20 20
wsj89 2.8
A especificação do sistema encontrada neste trabalho apresenta várias
carências para que o sistema se torne útil e competitivo na vida real, são
elas:
Interface
de interação mais poderosa
-
Permitir pesquisa orientada a registros (como o agrep) e não somente a linha.
-
Tornar mais flexível, permitindo o uso de partes adicionais ao padrão, tipo
consulta com definições de intervalos (1-4), conjuntos {x,y,z}, caracteres
coringas (?), etc;
-
Permitir que o usuário possa especificar que partes do padrão deveriam casar
exatamente e que partes poderiam ter erros. E mais, poder fornecer custos para
cada tipo de erros de maneira a permitir que tipo de erro mais o interessa;
-
Fornecer um help mais detalhado para suporte ao usuário;
-
Desenvolver uma interface gráfica.
Algoritmo
-
Melhorar a eficiência do algoritmo pesquisando e otimizando os que estão sendo
atualmente utilizados nas ferramentas de busca mais rápidas, como o agrep.
-
Agregar vários programas de busca com um algoritmo capaz de identificar através
da entrada do usuário qual seria o programa mais adequado para executar essa
busca. Isso permite aproveitar as vantagens de todos os algoritmos com o baixo
custo de analisar a entrada do usuário. Cada programa seria voltado para um
tipo de problema somente (baseado no tamanho das variáveis de entrada), podendo
ser muito mais eficiente, visto que soluções genéricas são sempre mais
complexas e sua abrangência limita sua eficiência.
4. Testes
Nossa implementação permite procurar por vários padrões ao mesmo tempo.
Consideramos as seguintes consultas que foram solicitadas para este trabalho:
Consulta 1 time ./wm 0 4 wsj89 DCC UFMG dollar
Consulta 2 time ./wm 0 4
wsj89 dia branco
Consulta 3 time ./wm 0 4 wsj89 Macunaima
administration
Consulta 4 time ./wm 0 4 wsj89 Brazilian coffee
Consulta 5 time ./wm 0 4 wsj89 New York Stock
Exchange
Consulta 6 time ./wm 0 4 wsj89 Manacapuru
Consulta 7 time ./wm 0 4 wsj89 Canada Treasury
Consulta 8 time ./wm 0 4 wsj89 Michael Gregory
Consulta 9 time ./wm 0 4 wsj89 price index
Consulta 1 time ./wmpas 0 wsj89 DCC UFMG dollar
…
Consulta 9
Consulta 1 time agrep -c DCC,UFMG,dollar wsj89
...
Consulta 9
Consulta 1 time ./bmh 4 wsj89 DCC UFMG dollar
...
Consulta 9
As consultas acima fazem parte de scripts usados durante a sessão
de testes. Correspondem a consultas com 0 erros e usando a opção 4 que mostra
somente o número de linhas com casamentos.
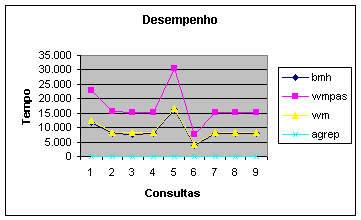
A seguir mostraremos os gráficos obtidos com estas consultas.
|
bmh |
wmpas |
wm |
agrep |
|
11.760 |
22.890 |
12.430 |
0.7 |
|
8.130 |
15.490 |
8.250 |
0.71 |
|
7.780 |
15.410 |
8.310 |
0.69 |
|
7.980 |
15.340 |
8.410 |
0.61 |
|
16.240 |
30.620 |
16.510 |
0.65 |
|
3.910 |
7.650 |
4.180 |
0.13 |
|
7.960 |
15.210 |
8.430 |
0.65 |
|
7.900 |
15.170 |
8.350 |
0.65 |
|
8.070 |
15.150 |
8.250 |
0.57 |
Gráfico
1: Comparação entre os desempenhos.
Mesmo admitindo k>1 essa relação
permanece. Avaliamos porque nos próximos gráficos.
Estudo
Empírico x Análise de Complexidade
Observando a complexidade obtida na análise das nossas implementações,
podemos perceber que o algoritmo BMH exige mais tempo quando aumentamos o
tamanho do padrão. Esse fato deveria ser imperceptível para o WM, pois WM
deveria ser sensível somente ao tamanho do erro. Isso nos motivou a testar separadamente
a variação de cada um destes parametros. Obtemos os seguintes gráficos:
|
ERRO |
|
|
|
erro=0,2,4,8
t=109MB m=14 |
||
|
Agrep |
WM |
WMPAS |
|
0.09 |
4.180 |
8.010 |
|
1.040 |
8.960 |
15.580 |
|
4.780 |
12.950 |
24.180 |
|
11.910 |
23.370 |
42.280 |
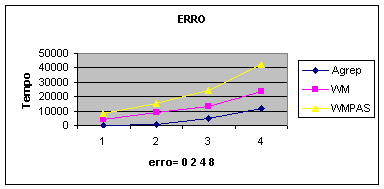
Gráfico
2: Variando somente o número de erros.
O gráfico 2 apresenta a queda de desempenho dos algoritmos com o aumento
no número de erros. Esta queda está ligada, também, com o aumento no número de
casamentos que aumenta junto com o número
k de erros, isso somente para o agrep que é sensível ao quanto que casa
o padrão (“m”), pois usa uma variação do BMH.
à WM = O(n.K)
|
TEXTO |
|
|
|
|
t=2.8 10 20 109MB err=0 m=5 |
|
||
|
Agrep |
BMH |
WM |
WMPAS |
|
0 |
0.1 |
0.1 |
0.21 |
|
0 |
0.36 |
0.39 |
0.67 |
|
0 |
0.71 |
0.73 |
1.380 |
|
0 |
4.040 |
4.040 |
7.480 |
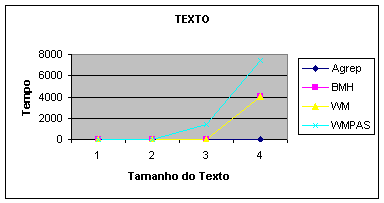
Gráfico
3: Variando somente o tamanho do texto.
O gráfico 3 ilustra o aumento do
tempo gasto para a pesquisa, com o aumento no tamanho do texto. O tempo
também varia com o número de casamentos para os sensíveis ao tamanho do padrão
como o BMH e, consequentemente, o agrep. Neste caso (diferente do anterior),
não necessariamente será um aumento diretamente proporcional ao tamanho do
texto (tamanho do erro). Ou seja, poderíamos ter um aumento no texto e, por
variar seu conteúdo, uma redução no número de casamentos. Isso poderia
compensar o tempo do BMH (agrep) para
arquivos maiores. No nosso gráfico tomamos o cuidado de ter um número de
casamentos quase igual para todos os tamanhos de arquivos usados, de forma que
isso seja uma constante e não altere a curva de crescimento.
à WM = O(N.k)
à BMH = O(N.m)
No próximo teste precisamos variar o tamanho do padrão, consequentemente
iremos variar o número de casamentos para um mesmo algoritmo. Ou seja, padrão
diferente implica em número de casamentos diferente. Para esse caso pegamos a
seguite amostra que não nos deu bons resultados:
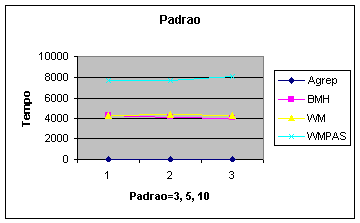
|
m=3,5,10 t=109MB erro=0 |
|
|
|
|
Agrep |
BMH |
WM |
WMPAS |
|
0.21 |
4.340 |
4.350 |
7.690 |
|
0.17 |
4.110 |
4.420 |
7.740 |
|
0.11 |
4.030 |
4.290 |
8.030 |
Gráfico
4: Variando somente o tamanho do padrão.
O gráfico 4 não mostra consideráveis alterações com o tamanho do padrão.
Isso aconteceu porque o número de
casamentos diminuiu com o aumento no tamanho do padrão. Com esse comportamente
quase que inversamente proporcional acabamos gerando um gráfico que parece
constante no tempo. Isso para BMH (agrep) pois o WM é insensível, realmente, ao
tamanho do padrão.
Para melhor análise pegamos um texto de tamanho 110MB composto somente
de caracteres “x” e procuramos os padrões p=yxx (m=3), p=yxxxxx (m=6) e
p=yxxxxxxxxxxx (m=12). Só assim, atingimos o pior caso obtido na análise de
complexidade e podemos perceber no gráfico como WM não é sensível à variação do
padrão /número de casamentos, por adotar um esquema de paralelismo de bits..
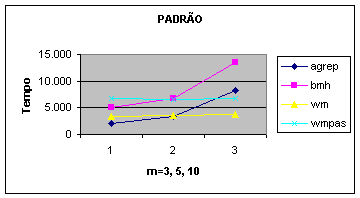
|
m=3 5 10 109MB erro=0 |
|
||
|
agrep |
bmh |
wm |
Wmpas |
|
2.110 |
5.000 |
3.360 |
6.830 |
|
3.430 |
6.810 |
3.500 |
6.610 |
|
8.200 |
13.500 |
3.660 |
6.670 |
Gráfico
4: Analisando o pior caso.
Observe que o que mostramos acima é
um caso onde não há casamentos de fato, mas a string é comparada o número
máximo de vezes até se perceber um erro.
Observe também que, como o agrep é
uma combinação de variantes destes algoritmos [WM 2]. Então ele é sensível a
todos os parametros (n, k e m). E
acompanha as mesmas alterações dos algoritmo sensível no momento.
A versão em Pascal do WM apresentou
um desempenho inferior aos resultados obtidos com a versão em C. Nossos
gráficos mostram um aumento não linear no valor de x da complexidade obtida.
à WM = O(n.k)
àWMPAS = O(n.k.X)
Apresentamos
a seguir gráficos comparando, diretamente, algumas operações lógicas das
linguagens.
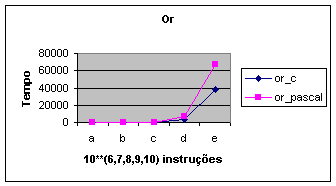
|
or_c |
0 |
0.04 |
0.38 |
3.780 |
37.980 |
|
or_pascal |
0 |
0.07 |
0.7 |
6.720 |
67.240 |
Gráfico
5: Operação Ou.
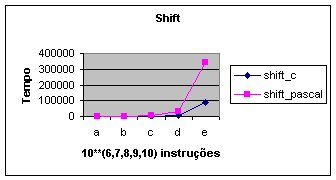
|
shift_c |
0.01 |
0.1 |
0.9 |
8.810 |
88.960 |
|
shift_pascal |
0.03 |
0.35 |
3.440 |
34.110 |
341.650 |
Gráfico
6: Operação de deslocamento.
Conclusão
O Agrep apresentou melhor desempenho
em todos os casos porque usa o melhor de cada algoritmo, por exemplo, para
casamento exato usa uma variação do BMH. Estudamos a sensibilidade de cada
algoritmo.
A versão em Pascal do WM apresentou
o pior desempenho como era de se esperar segundo [Ziviani]. Isso nos levou a
medir isoladamente o custo das operações lógicas em Pascal e compará-las
diretamente com as memas operações em C confirmando [Ziviani].
BIBLIOGRAFIA
[WM
1] Wu, Sun e Manber, Udi. Fast Searching Allowing Errors. Department of Computer
Science. University of Arizona.
[Baeza] Baeza-Yates, R.; Gonnet, Gaston H. Handbook
of Algorithms and Data Structures. Dept. of Computer Science, Univ. of Chile.
[Ziviani]
N. Ziviani. Processamento de Cadeia de Caracteres. Dept. de Ciência da
Computação, Univ. Federal de Minas Gerais, Brasil, 2003.
[Charras] Christian Charras, Thierry Lecroq.
Handbook of Exact String-Matching Algorithms. Université de Rouen Faculté
des Sciences et des Techniques, France.
[WM
2] Wu, Sun e Manber, Udi. AGREP - A Fast Approximate Pattern-Matching Tool. Department of Computer
Science. University of Arizona.
ANEXO
1
Listagem
completa dos programas implementados e
principais scripts utilizados nos testes.
Abaixo podemos visualizar o formato
do comando de linha para cada programa:
wm
= Shift-And com casamento aproximado em C
wm
= Shift-And com casamento aproximado em Pascal
bmh
= BMH (casamento exato)
Fomato
do comando de linha:
./wm erro opcao texto padrao_1 padrao_2 ...padrao_n
./bmh
opcao texto padrao_1 padrao_2 ...padrao_n
./wmpas erro texto padrao_1 padrao_2 ...padrao_n
Erro:
o numero de erros permitido
Padrao:
String sendo procurada no texto
Texto:
Arquivo texto onde buscamos o padrao
As
opções disponíveis nos algoritmos são:
1
quantidade total de casamentos no texto inteiro
2
exibe o numero das linhas com matches "inteiros" e as linhas
3
exibe o numero das linhas com matches e as linhas
4
quantidade de linhas que possuem pelo menos uma ocorrência do padrao
5
mostra a posição exata na linha onde ocorre o padrao
Obs.:
A opção 4 foi a única utilizada na fase
de testes, comparada a similar – c do grep/agrep.
A opção 2 de casamento inteiro procura o padrão entre espaços. Ocasiões
onde o padrão aparece no começo ou final da linha, acompanhado com sinais de
pontuação quaisquer ou situações similares, essa ocorrência não será
registrada.
Boyer-Moore-Horspool
(BMH)
Linguagem C
#include
<stdio.h>
#define MAX_ALPHABET_SIZE 256
#define MAX_SIZE 512
#define
MAX_FILE_NAME_SIZE 256
#define
MAX_LINE_SIZE 4096
#define
MAX_PATTERN_SIZE 29 /* considerando
uma palavra de 32 bits */
int opc; /* opcao de exibicao
no terminal de video*/
long bmh( pd, tx, n
)
/* (numero de
casamentos) bmh (padrao, linha do texto, tamanho da linha) */
char *pd, *tx;
int n;
{
int i, j, k, m,
d[MAX_ALPHABET_SIZE]; /* tabela de ocorrencias */
long match; /*
numero de casamentos */
m = strlen(pd);
if( m==0 ) return(1);
for( k=0; k<MAX_ALPHABET_SIZE; k++ )
d[k] = m; /* iniciando
tabela de ocorrencias com m */
for( k=0; k<m-1; k++ ) d[pd[k]] =
m-k-1;
/* atribuindo
deslocamento adequado para os caracteres do padrao*/
for( k=m-1; k < n; k += d[tx[k] &
(MAX_ALPHABET_SIZE-1)] ) {
/* efetua o
deslocamento */
for( j=m-1, i=k; j>=0 &&
tx[i] == pd[j]; j-- ) i--;
/* checando
casamento */
if( j == (-1) ) /*se houve casamento*/
if((opc==5)||(opc==1)){
/*
printf("MATCH posicao %d\n",k-m+1);*/
match++;
}else{
return(1);
/* retorna 1 quando
encontra o primeiro casamento */
}
}
return(match); /* retorna o numero de
casamentos ocorridos nesta linha do texto */
}
int main(int argc,
char *argv[]) {
FILE
*t; /* text file id */
long k,m,n,cont,c,match;
int
y;
char
line[MAX_LINE_SIZE], /*
linha do arquivo texto */
p[MAX_PATTERN_SIZE], /* padrao a ser pesquisado */
filename[MAX_FILE_NAME_SIZE]; /*
nome do arquivo texto */
if (argc < 4) { /* testa se o numero de
argumentos esta correto */
fprintf(stderr,
"Numero incorreto de parametros\n");
printf("
Fomato do comando de linha: \n");
printf(" ./bmh opcao texto padrao_1 padrao_2
...padrao_n \n");
printf(" Padrao: \n");
printf(" String
sendo procurada no texto\n");
printf(" Texto: \n");
printf(" Arquivo texto onde buscamos o padrao \n");
printf(" Opcao: \n");
printf(" 1 quantidade total de casamentos no texto inteiro\n");
printf(" 2
exibe o numero das linhas com matches e as linhas \n");
printf(" 3
exibe o numero das linhas com matches 'inteiros' e as linhas \n");
printf(" 4
quantidade de linhas que possuem pelo menos uma ocorrencia do padrao \n");
printf(" 5
mostra a posição exata na linha onde ocorre o padrao \n");
exit(1);
}
strcpy(filename, argv[2]);
opc=atoi(argv[1]);
for
(y=3;y<argc;y++)
{
strcpy(p, argv[y]); /* p recebe o padrao propriamente dito */
switch(opc){
case 3:
/* match
"inteiro" */
strcpy(p, "
"); /* p recebe um espaco como
primeiro caractere */
strcat(p, argv[1]); /* p recebe o padrao propriamente
dito */
strcat(p, " "); /* p recebe um espaco como ultimo
caractere */
break;
}
m = strlen(p); /* m armazena o tamanho do padrao*/
t =
fopen(filename, "r");
cont=0;
c=0;
while
(fgets(line, MAX_LINE_SIZE,t)){
cont++;
line[strlen(line)-1]='\0';
match =
bmh (p,line,strlen(line));
if (match!=0){
switch(opc){
case 1: /* quantidade total de casamentos no texto inteiro*/
c+=match;
break;
case 2: /* exibe o numero das linhas com matches e as linhas*/
printf("match na linha %d \n
%s\n",cont,line);
break;
case 3: /* exibe o numero das linhas com matches "inteiros" e
as linhas*/
printf("Match inteiro na linha
%d \n %s\n",cont,line);
break;
case 4: /* quantidade de
linhas que possuem pelo menos uma ocorrência do padrao */
c++;
break;
case 5: /* mostra a
posição exata na linha onde ocorre o padrao */
printf("linha %d
\n",cont);
break;
default: printf("%s: %s\n",
filename, line); /*mostra o nome do arquivo e a linha*/
}
}
}
if ((opc==4)||(opc==1))
/*printf("%d\n",c)*/;
}
close(t);
}
Algoritmo Wu e Manber (WM)
Linguagem C
#include
<stdio.h>
#define TRUE 1
#define FALSE 0
#define ALPHABET_SIZE 256
#define
MAX_LINE_SIZE 512
#define
MAX_MODIFIED_LINE_SIZE 512
#define
MAX_PATTERN_SIZE 29
#define
MAX_NUMBER_OF_ERRORS 28
#define
MAX_FILE_NAME_SIZE 256
long
S[ALPHABET_SIZE], /* mascaras
dos caracteres do alfabeto*/
valid[ALPHABET_SIZE], /* diz se o caractere faz parte de
palavras */
Start[MAX_NUMBER_OF_ERRORS], /* mascaras
de inicializacao */
M; /* mascara que diz onde a busca
obrigatoriamente e' exata no
padrao*/
/* Funcao : preproc
Objetivos : preprocessar o padrao, montando
as mascaras de
inicializacao, dos caracteres
do alfabeto e a de busca
exata obrigatoria
Parametros: o padrao e o numero de erros
Saida
: nenhuma */
void preproc(char
*p, long k) {
int i,
j,
m; /* pattern size */
m = strlen(p);
for (i = 0; i < (k + 1); i++) {
Start[i] = 0; /* zerando a mascara de
inicializacao dos Rs */
for
(j = 0; j <= i; j++) {
Start[i] |= 1 << (m - j); /* construindo os automatos de forma a
permitir
um numero de erros <=k*/
}
}
for (i = 0; i < ALPHABET_SIZE; i++) {
S[i] = 0; /*
zerando a mascara de caracteres do alfabeto */
valid[i] = ((i >= 'a') && (i
<= 'z')) || ((i >= 'A') && (i <= 'Z'));
/* registrando os caracteres que fazem
parte do alfabeto usado*/
}
M = 0;
for (i = 0; i < m; i++) { /* inicializa
mascaras de caracteres do
alfabeto */
if (((p[i] >= 'a') && (p[i]
<= 'z')) || ((p[i] >= 'A') && (p[i] <='Z'))) {
S[p[i]] |= 1 << (m - 1 - i);
/* marca com 1
todas as ocorrencias de p[i] no padrao */
M |= 1 << (m - 1 - i);
/* marca com 1
todas as posicoes dos caracteres do padrao para busca
exata*/
}
else {
S[' '] |= 1 << (m - 1 - i);
/* S contem 1 em
todas as posicoes cujo caracter nao faz parte do
alfabeto*/
}
}
for (i = 0; i < ALPHABET_SIZE; i++) {
if (!valid[i]) {
S[i] = S[' '];
/* caso i nao faz
parte do alfabeto recebe a mascara constuida em S[' ']
*/
}
}
}
/* Funcao : Wu_Manber
Objetivos : verifica se um padrao ocorre ou
nao numa sequencia, com um
numero de erros menor ou igual
a k
Parametros: o padrao, a sequencia e o numero
de erros
Saida
: verdadeiro se o padrao ocorre na sequencia ou falso, caso
contrario */
long Wu_Manber(char
*p, char *t, long k) {
long i,
j,
m, /* tamanho do padrao */
n, /*
tamanho da sequencia */
matchfound, /* diz se um casamento foi encontrado */
R0[MAX_NUMBER_OF_ERRORS], /* mascaras
de estado anterior */
R1[MAX_NUMBER_OF_ERRORS]; /* mascaras
de estado atual */
char newt[MAX_MODIFIED_LINE_SIZE]; /*
sequencia entre espacos */
long count; /* registra a quantidade de matches ocorridos */
strcpy(newt, " ");
strcat(newt, t);
strcat(newt, " ");
n = strlen(newt);
m = strlen(p);
matchfound = FALSE;
for (i = 0; i <= k; i++) { /* inicializa
mascaras de estado */
R1[i] = Start[i];
R0[i] = Start[i];
}
count=0;
for (i = 0; i < n; i++) { /* executa o
algoritmo */
R1[0] = ((R0[0] >> 1) &
S[newt[i]]) | (Start[0] & R0[0]);
/*checando casamento
inteiro */
for (j = 1; j <= k; j++) {
/*checando
casamento com erro */
R1[j] = ((R0[j] >> 1) &
S[newt[i]]) | ((R0[j-1] | ((R1[j-1] | R0[j-1]) >> 1)) & M) |
(Start[0] & R0[j]);
}
for (j = 0; j <= k; j++) { /* atribui
estado atual no anterior */
R0[j] = R1[j];
if (R1[j] & 1) { /* se bit menos
significativo estiver ativo, entao
tem-se um casamento
na linha atual do texto */
/* printf("casou na posicao:
%d\n",i); */
matchfound = TRUE;
count+=1;
}
}
}
return count;
}
int main(int argc,
char *argv[]) {
FILE *t; /* text file id
*/
char
line[MAX_LINE_SIZE], /* linha do arquivo texto*/
p[MAX_PATTERN_SIZE], /* padrao a
ser pesquisado*/
filename[MAX_FILE_NAME_SIZE]; /* nome do arquivo texto*/
int
opc, /* opcao de exibicao o terminal*/
c, /*acumulador
de ocorrencias do padrao no texto inteiro*/
cont; /* contador
de linhas do texto */
long i,
j,
m, /*
tamanho do padrao */
k, /*
numero de erros */
match, /* numero de casamentos */
y;
printf(" ");
if (argc < 5) { /* testa se o numero de
argumentos esta correto */
fprintf(stderr, "Numero
incorreto de parametros\n");
printf(" Fomato do comando de
linha: \n");
printf(" ./wm erro opcao texto padrao_1 padrao_2
...padrao_n \n");
printf(" Erro: \n");
printf(" o numero de erros permitido \n");
printf(" Padrao: \n");
printf(" String
sendo procurada no texto\n");
printf(" Texto: \n");
printf(" Arquivo texto onde buscamos o padrao \n");
printf(" Opcao: \n");
printf(" 1 quantidade total de casamentos no texto inteiro\n");
printf(" 2
exibe o numero das linhas com matches e aslinhas \n");
printf(" 3
exibe o numero das linhas com matches 'inteiros'e as linhas \n");
printf(" 4
quantidade de linhas que possuem pelo menos umaocorrencia do padrao \n");
printf(" 5
mostra a posição exata na linha onde ocorre opadrao \n");
exit(1);
}
k = atoi(argv[1]);
if (k > MAX_NUMBER_OF_ERRORS) { /* valida
o numero de erros da busca */
fprintf(stderr, "Numero de erros
maior que o maximo permitido\n");
exit(1);
}
strcpy(filename, argv[3]);
opc=atoi(argv[2]);
for
(y=4;y<argc;y++)
{
strcpy(p, argv[y]); /* p recebe o padrao
propriamente dito */
m = strlen(p); /* m armazena o tamanho do
padrao */
switch(opc){
case 3: //match inteiro
strcpy(p, " "); /* p recebe
um espaco como primeiro caractere */
strcat(p, argv[4]); /* p recebe o
padrao propriamente dito */
strcat(p, " "); /* p recebe
um espaco como ultimo caractere */
break;
}
if (m > MAX_PATTERN_SIZE - 2) {
fprintf(stderr, "Tamanho do padrao
maior que o maximo permitido\n");
exit(1);
}else
if (m > MAX_PATTERN_SIZE) { /* valida o
tamanho do padrao */
fprintf(stderr, "Tamanho do padrao
maior que o maximo permitido\n");
exit(1);
}
if (k >= m) {
fprintf(stderr, "Numero de erros nao
e menor que o tamanho do padrao\n");
exit(1);
}
preproc(p, k);
t = fopen(filename, "r");
c=0;
cont=0;
while(fgets(line, MAX_LINE_SIZE, t)) {
line[strlen(line) - 1] = '\0';
cont+=1;
if (match=Wu_Manber(p, line, k)) {
switch(opc){
case 1: /* quantidade total de
casamentos no texto inteiro*/
c+=match;
break;
case 2: /* exibe o numero das linhas
com matches e as linhas*/
printf("match na linha %d \n
%s\n",cont,line);
break;
case 3: /* exibe o numero das linhas
com matches
"inteiros" e
as linhas*/
printf("Match inteiro na linha
%d \n %s\n",cont,line);
break;
case 4: /* quantidade de linhas que possuem pelo menos uma
ocorrência
do padrao */
c++;
break;
case 5: /* mostra a posição exata na
linha onde ocorre o padrao*/
printf("linha %d \n",cont);
break;
default: printf("%s: %s\n",
filename, line);
}
}
}
if ((opc==1)||(opc==4))
/*printf("%d\n",c)*/;
}
close(t);
}
Algoritmo Wu e Manber (WM)
Linguagem
Pascal
program ShiftAndAprox(output);
const
TAM_TEXTO = 1000000;
TAM_ALFABETO= 255;
TAM_PADRAO = 10;
TAM_REGISTRO= 10;
var
p : String[TAM_PADRAO];
T : String[TAM_TEXTO];
k,r,i : integer;
matchs, lastbit:integer;
F
: text;
Masc: array[0..TAM_ALFABETO]of
integer;
procedure shiftAndPreprocess (p:String);
var j, bit, a,
m: integer;
begin
{pre-processamento}
for
j:=ord('a') to ord('z') do
Masc[j] :=
0;
for
j:=ord('A') to ord('Z') do
Masc[j] :=
0;
bit := 1;
m :=
length(p);
for j:=1 to m
do begin
a :=
ord(p[j]);
Masc[a] :=
Masc[a] or bit;
lastbit :=
bit;
bit := bit
shl 1;
end;
end;
procedure shiftAndSearch (var k:integer; var
T,p:String);
var m, n: integer;
i, j ,a: integer;
R
: array[0..m]of integer;
Rant, Rnovo: integer;
bit
, bitaux: integer;
begin
{pesquisa}
for j:=1 to m
do
R[j] :=
0;
n :=
length(T);
bit := 0;
bitaux:= 1;
for j:=1 to k
do begin
R[j] := bit;
bit
:= (bit shl 1)or bitaux;
bitaux :=
bitaux or bit;
end;
bit := 0;
for i:=1 to n
do begin
Rant :=
bit;
Rnovo :=
((Rant shl 1) or 1) and Masc[ord(T[i])];
bit :=
Rnovo;
for j:=1 to
k do begin
Rnovo :=
((R[j] shl 1) and Masc[ord(T[i])])or Rant or ((Rant or Rnovo) shl 1);
Rant := R[j];
R[j] := Rnovo;
end;
if ((Rnovo
and lastbit)<>0) then begin
{ Writeln("casou na posicao:
",i);}
matchs
:= matchs + 1;
end;
end;
end;
{programa principal}
Begin
if
ParamCount < 3 then begin
writeln("./wmpas
erro texto padrao");
halt(1);
end;
T :=
ParamStr(2);
Val(ParamStr(1),k,r);
assign(F,T);
for i:=3 to
ParamCount do
begin
p := ParamStr(i);
reset(F);
matchs :=
0;
shiftAndPreprocess(p);
while not
EOF(F) do
begin
readln(F,T);
shiftAndSearch(k,T,p);
End;
writeln(matchs);
end;
close(F);
end.
TESTES (scripts)
1- Variando o
tamanho do ERRO.
echo Agrep err=0 2
4 8 109MB m=14
time agrep -c administration wsj88
time agrep -c -2 administration wsj88
time agrep -c -4 administration wsj88
time agrep -c -8 administration wsj88
echo wm err=0 2 4 8
109MB m=14
time ./wm 0 4 wsj88 administration
time ./wm 2 4 wsj88 administration
time ./wm 4 4 wsj88 administration
time ./wm 8 4 wsj88 administration
echo wmpas err=0 2
4 8 109MB m=14
time ./wmpas 0 wsj88 administration
time ./wmpas 2 wsj88 administration
time ./wmpas 4 wsj88 administration
time ./wmpas 8 wsj88 administration
2- Variando o
tamanho do PADRAO.
echo agrep m=3 5 10
109MB err=0
time agrep -c dia wsj88
time agrep -c price wsj88
time agrep -c Manacapuru wsj88
echo bmh m=3 5 10
109MB err=0
time ./bmh 4 wsj88 dia
time ./bmh 4 wsj88 price
time ./bmh 4 wsj88 Manacapuru
echo wm m=3 5 10
109MB err=0
time ./wm 0 4 wsj88 dia
time ./wm 0 4 wsj88 price
time ./wm 0 4 wsj88 Manacapuru
echo wmpas m=3 5 10
109MB err=0
time ./wmpas 0 wsj88 dia
time ./wmpas 0 wsj88 price
time ./wmpas 0 wsj88 Manacapuru
3- Variando o
tamanho do TEXTO.
echo agrep t=2.8 10 20 109MB err=0 m=5
time agrep -c index wsj89
time agrep -c index wsj88_10
time agrep -c index wsj88_10
time agrep -c index wsj88
echo bmh t=2.8 10
20 109MB err=0
time ./bmh 4 wsj89 index
time ./bmh 4 wsj88_10 index
time ./bmh 4 wsj88_20 index
time ./bmh 4 wsj88 index
echo wm t=2.8 10 20
109MB err=0
time ./wm 0 4 wsj89 index
time ./wm 0 4 wsj88_10 index
time ./wm 0 4 wsj88_20 index
time ./wm 0 4 wsj88 index
echo wmpas t=2.8 10
20 109MB err=0
time ./wmpas 0 wsj89 index
time ./wmpas 0 wsj88_10 index
time ./wmpas 0 wsj88_20 index
time ./wmpas 0 wsj88 index