

CURSO DE PÓS-GRADUAÇÃO EM CIÊNCIA DA COMPUTAÇÃO
PROJETO E ANÁLISE DE ALGORITMOS
Última alteração: July 12, 2004
Professor:
Nivio Ziviani
Monitor:
Fabiano C. Botelho
1
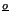
Trabalho Prático - 18/03/04 - 10 pontos
Data de Entrega: 07/04/04
Penalização por Atrazo: 1 ponto até 16/04/04 mais 1 ponto por dia útil
a seguir
Observação: Toda a documentação deverá ser apresentada como uma página
acessível via Web (apresente o link para acesso à documentação).
- Avaliar as somas (0,5 + 0,5 + 0,5 + 0,5 + 0,5 pontos):
-
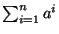
-
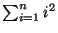
-
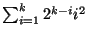
-
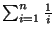
-
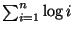
- Apresente a complexidade de tempo para os procedimentos:
(0,5 + 0.5 + 0.5 + 0.5 pontos)
PROCEDURE FazAlgo ( n : integer);
VAR i, j, k, x : integer;
BEGIN
x := 0;
FOR i := 1 TO n DO
FOR j := i + 1 TO n - 1 DO
FOR k := 1 TO j DO x := x + 1;
END;
Pesquisa(n);
IF n <= 1
THEN termine
ELSE BEGIN
ordena os n elementos;
{ de alguma forma isto permite descartar 1/3 dos }
{ elementos e fazer uma chamada recursiva no resto }
Pesquisa (2n/3);
END;
PROCEDURE Sort (VAR A: ARRAY[1..n] OF integer; i, j: integer);
{ n uma potencia de 3 }
BEGIN
IF i < j
THEN BEGIN
m := (i + j - 1)/3;
Sort (A,i,m);
Sort (A,m+1,j);
Merge (A,i,m,j);
{ Merge intercala A[i..m] e A[m+1..j] em A[i..j] a um custo n}
END;
END;
PROCEDURE D ( VAR L );
BEGIN
IF |L| > 1
THEN BEGIN
Divide L em 3 partes iguais L1, L2, L3 com custo
de |L| * |L| * |L| passos; {|L| ao cubo}
D(L1); D(L2); D(L3);
END;
END;
- Limite inferior:
(1 + 0.5 + 1 + 0.5 pontos)
- Apresente um algoritmo para encontrar o maior e o
segundo maior elemento de um conjunto.
- Seja
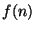 o número de comparações realizadas pelo seu algoritmo.
Apresente a análise da complexidade de tempo do seu algoritmo.
o número de comparações realizadas pelo seu algoritmo.
Apresente a análise da complexidade de tempo do seu algoritmo.
- Determine o limite inferior para o problema de encontrar o maior e o
segundo maior elemento de um conjunto.
- O algoritmo apresentado no item (a) é ótimo?
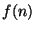 é um limite assintótico firme?
Justifique sua resposta.
é um limite assintótico firme?
Justifique sua resposta.
- Shellsort
(1 + 1 + 0,5 pontos)
O objetivo deste trabalho é realizar um estudo
do algoritmo Shellsort de ordenação interna
(Ziviani, 2004).
- Determine experimentalmente o número esperado de (i) comparações
e (ii) movimento-de-registros.
Utilize arquivos de diferentes tamanhos com chaves geradas randomicamente.
Use o programa Permut.c para obter uma
permutação randômica de 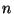 valores (Ziviani, 2004, pag. 427).
Repita
cada experimento algumas vezes e obtenha a média para cada medida
de complexidade.
valores (Ziviani, 2004, pag. 427).
Repita
cada experimento algumas vezes e obtenha a média para cada medida
de complexidade.
- Dê a sua interpretação dos dados obtidos,
comparando-os com as conjecturas relatadas em Ziviani (2004, pag. 102).
- Procure trabalhos relacionados na literatura
com resultados analíticos (se houver) e descreva suscintamente esses trabalhos.
Como os resultados experimentais que você obteve comparam com os resultados
analíticos encontrados na literatura?
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 pa04tp1
The translation was initiated by Nivio Ziviani on 2004-07-12


Nivio Ziviani
2004-07-12