

CURSO DE PÓS-GRADUAÇÃO EM CIÊNCIA DA COMPUTAÇÃO
PROJETO E ANÁLISE DE ALGORITMOS
Última alteração: July 12, 2004
Professor:
Nivio Ziviani
Monitor:
Fabiano C. Botelho
2
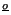
Trabalho Prático - 15/04/04 - 10 pontos
Data de Entrega: 03/05/04
Penalização por Atrazo: 1 ponto até 07/05/04 mais 1 ponto por dia útil
a seguir
Observação: Toda a documentação deverá ser apresentada como uma página
acessível via Web (apresente o link para acesso à documentação).
Problema da Mochila [Z04], [HS78]
Um escoteiro-mirim se prepara para um acampamento e neste momento, em fase
final de preparativos, ele vai colocar os embrulhos dentro de sua mochila.
Mal ele começou, já notou que deverá deixar alguns itens para trás,
pois como ele vai caminhar muito, o peso de sua mochila não deverá
execeder um limite de 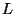 quilos. Para auxiliar no processo de decidir quais
itens levar, ele assinalou a cada um deles, um valor que representa a sua
utilidade. O problema da mochila é então o problema de
decidir, em função das suas utilidades, quais itens levar
de modo a não sobrecarregar a mochila.
quilos. Para auxiliar no processo de decidir quais
itens levar, ele assinalou a cada um deles, um valor que representa a sua
utilidade. O problema da mochila é então o problema de
decidir, em função das suas utilidades, quais itens levar
de modo a não sobrecarregar a mochila.
Outra situação ilustra o mesmo problema.
Uma pessoa recebe um prêmio que permite escolher quaisquer dos
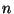 itens em uma loja.
O i-ésimo item tem valor
itens em uma loja.
O i-ésimo item tem valor 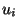 reais e pesa
reais e pesa 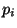 quilos
(
quilos
(
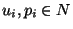 ).
A restrição do prêmio é que a pessoa tem que levar consigo
uma mochila que pode carregar
até
).
A restrição do prêmio é que a pessoa tem que levar consigo
uma mochila que pode carregar
até 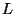 quilos e
quilos e
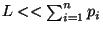 .
Determine o conjunto de itens que a pessoa deve colocar na
mochila de forma que ela consiga carregá-los todos dentro da mochila e
o valor total dos itens seja maximizado.
.
Determine o conjunto de itens que a pessoa deve colocar na
mochila de forma que ela consiga carregá-los todos dentro da mochila e
o valor total dos itens seja maximizado.
Enunciando este problema em termos mais formais:
É dado um conjunto 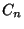 de
de 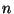 itens, representado por
itens, representado por
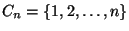 ,
cada item
,
cada item 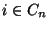 tem um peso
tem um peso 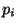 e utilidade
e utilidade
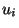 (
(
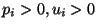 ).
Desejamos determinar um subconjunto
).
Desejamos determinar um subconjunto
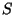 dos itens tal que a soma dos pesos dos elementos de
dos itens tal que a soma dos pesos dos elementos de 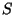 seja menor ou igual
a capacidade da mochila
seja menor ou igual
a capacidade da mochila 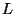 e que a utilidade total dos elementos de
e que a utilidade total dos elementos de 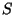 seja a maior possível. Matematicamente:
seja a maior possível. Matematicamente:
O que fazer
- Prove que este problema é
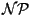 -Completo.
-Completo.
- Apresente três algoritmos alternativos para solucionar o problema da mochila,
utilizando três paradigmas de projeto de algoritmos,
o primeiro utilizando tentativa e erro (backtracking),
o segundo utilizando programação dinâmica e o
terceiro utilizando uma estratégia gulosa.
- Os algoritmos levam sempre à solução ótima? (Discuta a questão separadamente para cada algoritmo)
- Implemente cada um de seus algoritmos.
- Execute cada algoritmo para valores de
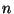 crescentes
(e.g.,
crescentes
(e.g., 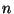 =10,50,100,200,300,400,500). Para cada valor de
=10,50,100,200,300,400,500). Para cada valor de 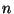 ,
faça experimentos com valores de
,
faça experimentos com valores de 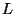 também variados mas limitados a 50% da soma dos pesos de todos os itens,
isto é,
também variados mas limitados a 50% da soma dos pesos de todos os itens,
isto é,
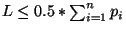 . Para cada entrada, discuta
os resultados obtidos com cada algoritmo em termos do tempo de execuão e precisão da resposta. Mostre gráficos
que contraste estas medidas para os três algoritmos.
Os valores de
. Para cada entrada, discuta
os resultados obtidos com cada algoritmo em termos do tempo de execuão e precisão da resposta. Mostre gráficos
que contraste estas medidas para os três algoritmos.
Os valores de 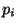 e
e 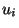 deverão ser gerados
aleatoriamente utilizando os comandos:
deverão ser gerados
aleatoriamente utilizando os comandos: 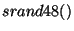 e
e 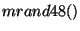 .
Assuma que os elementos devem estar no interval [-MAX..MAX], onde
MAX é uma constante do programa.
.
Assuma que os elementos devem estar no interval [-MAX..MAX], onde
MAX é uma constante do programa.
O que deve ser apresentado:
- A prova de que este problema é
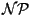 -Completo.
-Completo.
- Listagem do programa para a solução backtracking.
Uma descrição breve do algoritmo e das estruturas de dados
utilizadas, a análise do algoritmo,
bem como o relato sobre o tamanho do maior problema resolvido.
- Listagem do programa para a solução por programação
dinâmica.
Uma descrição breve do algoritmo e das estruturas de dados
utilizadas, a análise do algoritmo,
bem como o relato sobre o tamanho do maior problema resolvido.
- Listagem do programa para a solução gulosa.
Uma descrição breve do algoritmo e das estruturas de dados
utilizadas, a análise do algoritmo, bem como um
exemplo que não produza a solução ótima.
- Submeta eletronicamente a implementação dos três algoritmos.
Maiores detalhes sobre a documentação das implementações realizadas,
bem como submeter eletronicamente as implementações, podem ser vistos em
instruções para a entrega de trabalhos praticos).
Distribuição dos Pontos:
- Prova de que este problema é
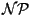 -Completo: 2
-Completo: 2
- mostrar que problema pertence a
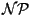 : 0.5
: 0.5
- redução polinomial a partir de outro problema
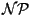 -Completo: 1.5
-Completo: 1.5
- Solução backtracking: 2
- Solução por progração dinâmica: 3
- Solução heurística: 3
This document was generated using the
LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 pa04tp2
The translation was initiated by Nivio Ziviani on 2004-07-12


Nivio Ziviani
2004-07-12