Análise de Complexidade de Métodos Numéricos para Interpolação

 

Bianca Costa Guimarães e Luiz Thomaz de Nascimento

 

Departamento de Ciência da Computação do ICEx -- Universidade Federal de Minas Gerais

Caixa Postal 702, 30.123-970 Belo Horizonte--MG

bianca@dcc.ufmg.br

lthomaz@dcc.ufmg.br

 

Resumo

 

Este trabalho, tem como objetivo apresentar uma revisão das análises numéricas aplicadas ao problema de interpolação. Os métodos numéricos de interpolação possuem uma aplicação direta na análise numérica de complexidade de algoritmos. Neste trabalho, serão apresentados métodos seqüenciais de Newton, Lagrange e Gregory-Newton. Serão apresentadas suas respectivas complexidades de avaliação e um estudo comparativo dos mesmos. Também será apresentado, para problemas de ordem superior, o algoritmo paralelo de interpolação de Newton.

 

 

1 -     Introdução

 

No estudo de projeto e análise de algoritmos, desenvolve-se técnicas para fazer análise de complexidades. Esta análise tem papel decisivo para o projeto de algoritmos eficientes. Muitas vezes analisar um algoritmo não é uma tarefa fácil, pois envolve manipulações de somas, equações de recorrência e outros cálculos matemáticos de difícil desenvolvimento. Sendo assim os método numéricos podem ser uma alternativa de avaliação de complexidades de algoritmos, especialmente nos casos em que a análise exata é difícil ou envolve probabilidades. Assim, este texto apresenta métodos de interpolação seqüenciais e paralelos que podem ser utilizados nestes estudos.

 

Na seção 2, é descrito brevemente o conceito de complexidade de algoritmos. Na seção 3 são apresentados 3 métodos numéricos seqüenciais de interpolação a saber, Gregory-Newton, Newton e Lagrange com suas respectivas complexidades de computação. A seção 4 mostra um estudo comparativo referente as complexidades de cada um dos métodos apresentados. Na seção 5 veremos uma análise de complexidade de um algoritmo utilizando o método seqüencial de Newton. Na seção 6 é apresentado o método numérico paralelo de interpolação de Newton e algumas considerações referentes à sua implementação. Finalmente na seção 7 é mostrado as conclusões e considerações sobre a aplicação dos métodos numéricos de interpolação.

 

 

2 -     Análise de complexidade

 

É importante, quando avaliamos a eficiência de um algoritmo qualquer, sabermos como se comporta o número de operações relevantes do algoritmo em função do tamanho de sua entrada. Este comportamento é chamado de análise de complexidade de tempo do algoritmo. Quando avaliamos a quantidade de memória necessária em função do tamanho da entrada, denominamos análise de complexidade de espaço. Existe uma vasta teoria sobre técnicas de avaliação formal destas complexidades [1]. Muitas vezes as manipulações algébricas envolvidas nestas avaliações são complexas e nestes casos pode-se utilizar métodos numéricos para inferir sobre os comportamentos dos algoritmos.

3 -     Métodos Seqüências de Interpolação

 

Seja uma tabela com valores de x e y associados. Para se obter o valor de y para um dado x não constante na  tabela é necessário encontrar uma função que relaciona estas variáveis. As funções mais utilizadas para determinar estas relações são os polinômios. Um polinômio construído com o intuito de aproximar uma função é denominado polinômio interpolador. Existem vários métodos para construir um polinômio interpolador a partir de um conjunto de pares de dados. Será apresentado a seguir uma ferramenta para construir um polinômio interpolador de Lagrange, Newton e Gregory-Newton.

 

3.1 -     Método de Lagrange

 

Sejam dados n + 1 pontos (, sendodistintos, tais que e . Deseja-se construir um polinômiode grau não superior a n e possuindo nos pontos  o mesmo valor da função isto é,

Tem-se a fórmula do polinômio interpolador de Lagrange de grau n  

 

 

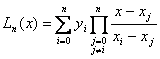
Por exemplo, a fórmula de Lagrange com n=2, torna-se:

 

 

Temos abaixo a complexidade da interpolação de Lagrange para um um polinômio de grau n com relação ao número de operações:

 

Operações

Complexidade

Adições

Multiplicações

Divisões

n+1

 

3.2 -     Método de Newton

 

Como visto no item anterior, os polinômios de Lagrange constituem um modo de interpolar sem a necessidade de resolver um sistema de equações lineares. Será mostrado, a seguir, um esquema alternativo para a construção de um polinômio interpolador.   

 

Operador de diferença dividida

 

Seja a função y = f(x) cujo gráfico passa pelos pontos i = 0,1,2,...,n. O operador de diferença dividida D é definido como sendo

 

a) ordem 0: 

 

b) ordem 1:

 

c) ordem 2:  

 

d) ordem n:

 

O teorema 3.2 mostra uma importante propriedade das diferenças divididas de um polinômio. Essa propriedade é fundamental para a construção dos polinômios de Newton.

Teorema 3.2   Se y=f(x) for um polinômio de grau n então suas diferenças divididas de ordem n+1 são identicamente nulas, isto é, .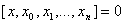

 

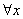Fórmula de Newton

 

Fazendoe usando a notação de diferenças divididas com o operador D, tem-se o polinômio de Newton de grau n.

 

ou

 

Temos abaixo a complexidade da interpolação de Newton para um um polinômio de grau n com relação ao número de operações:

 

Operações

Complexidade

Adições

Multiplicações

n

Divisões

 

3.3 -     Método de Gregory-Newton

 

Quando os valores das abscissas forem igualmente espaçados, a formula de Newton pode ser simplificada, resultando na formula de Gregory-Newton. Portanto, o polinômio de Gregory-Newton é um  caso particular do polinômio de Newton para pontos igualmente espaçados.  

 

Operador de diferença finita ascendente

 

Seja a função y = f(x) que passa pelos pontos i = 0,1,2,...,n, sendo . O operador de diferença finita ascendente D é definido como sendo

 

a) ordem 0: 

 

b) ordem 1:

 

c) ordem 2:  

 

d) ordem n:

 

 

Fórmula de Gregory-Newton

 

Fazendoe usando a notação de diferenças finita ascendente com o operador D, tem-se o polinômio de Gregory-Newton de grau n

.

,

 

onde utiliza-se uma variável auxiliar

ou

 

Temos abaixo a complexidade da interpolação de Gregory-Newton para um polinômio de grau n com relação ao número de operações:

 

Operações

Complexidade

Adições

Multiplicações

n

Divisões

n+1

 

 

4 -     Estudo Comparativo dos Métodos Seqüenciais

 

Como vimos na seção anterior cada um dos métodos numéricos possui um número específico de operações aritméticas que podem ser resumidos na tabela abaixo:

 

Método Numérico

Número de Operações Aritméticas

Adições

Multiplicações

Divisões

Lagrange

n+1

Gregory-Newton

n

Newton

n

 

Analisando a tabela acima não podemos afirmar diretamente qual é o método que possui o menor custo de computação. Isto deve-se ao fato de que em geral, um adição gasta menos ciclos de máquina que uma multiplicação que gasta menos ciclos que uma divisão.

A dependência dos tempos de ciclos em relação a arquitetura de máquina utilizada é um fator importante a ser considerado na análise de eficiência dos métodos apresentados acima. 

Foram implementados os 3 métodos utilizando o software MATLAB. Utilizando um conjunto de pontos a serem interpolados foram feitas várias simulações contabilizando o tempo de CPU gasto na execução de cada um do métodos. As simulações foram feitas utilizando uma máquina PC 400Mhz. Os resultados podem ser sintetizados na figura abaixo.

 

 

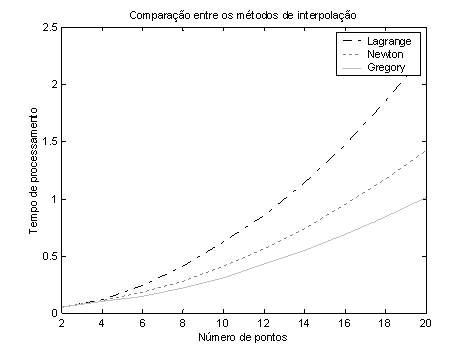
Fig. 1 – Tempo de processamento dos métodos seqüências de interpolação

 

Na figura 1 podemos verificar que o método Gregory-Newton é o mais eficiente para a arquitetura PC. A desvantagem na utilização deste método, é a exigência de que as abscissas dos pontos a serem utilizados para o polinômio interpolador de grau n, devam ser necessariamente eqüidistante.

 

 

5 -     Análise de Algoritmos Polinomiais

 

Nesta seção será aplicada a técnica de análise de complexidade de algoritmos polinomiais utilizando interpolação de Newton. Esta técnica só poderá ser utilizada para algoritmos que independam do conteúdo da entrada de dados. Apresenta-se abaixo a análise clássica de complexidade e a análise via interpolação de Newton. Os valores das diferenças divididas necessárias foram calculados utilizando uma implementação no MATLAB.

 

5.1 -     Algoritmo da função Máximo - Mínimo

 

Algoritmo MaximoMinimo(A,Inf,Sup,Min,Max)

/* Objetivo: Encontra simultaneamente o maior e o menor elemento de Arranjo A

    A → Arranjo com os elementos

    Inf,Sup → índices dos limites inferior e superior  */

 

(1)      se (Sup – Inf) £ 1 então

(2)               se A(Inf) < A(Sup) então

(3)                        Max = A(Sup)

(4)                        Min = A(Inf)

(5)               senão

(6)                        Max = A(Inf)

(7)                        Min = A(Sup)

(8)               fim se

(9)      senão

(10)           Meio = (Sup + Inf) % 2  /*  divisão inteira */

(11)           MaximoMinimo(A,Inf,Meio,Maximo1,Minimo1)

(12)           MaximoMinimo(A,Meio+1,Sup,Maximo2,Minimo2)

(13)           se Maximo1 > Maximo2 então

(14)                    Max = Maximo1

(15)           senão

(16)                    Max = Maximo2

(17)           fim se

(18)           se Minimo1 > Minimo2 então

(19)                    Min = Maximo2

(20)           senão

(21)                    Max = Maximo1

(22)           fim se

(23)  fim se

Fim Algoritmo

                     

Análise Clássica

 

Será tomada como medida de custo relevante o número de comparações entre os elementos do vetor A. Logo,

T(n)=1,                                             para n £ 2;

T(n)= T ( ën/2û ) + T ( én/2ù ) + 2 ,  para n >2.

 

Resolvendo esta relação de recorrência, tem-se que:

 

 

Análise via interpolação de Newton

 

A função MaximoMinino foi implementada e os testes foram realizados utilizando vetores de entrada com tamanhos de , k = 2,...,5. Estes valores foram armazenados em um vetor x. Para cada  foi obtido um respectivo custo de complexidade e armazenado na i-ésima posição do vetor y. Para obter este custo introduziu-se no algoritmo um contador, incrementado-o a cada comparação realizada entre os elementos do vetor. A partir dos vetores x e y construiu-se a tabela de diferenças divididas.

 

i

0

4

4

3/2

0

1

8

10

3/2

0

2

16

22

3/2

 

3

32

46

 

 

 

Analisando a tabela, observa-se que as diferenças divididas de ordem 2 são identicamente nulas. Logo, o polinômio interpolador tem grau 1, ou seja, este algoritmo apresenta complexidade linear.

Para determinar as constantes deste polinômio é utilizada a fórmula de Newton

 

 

 

Assim, o custo total para executar este programa com entrada de tamanho n será

 

 

Como pode-se observar o custo de complexidade via interpolação de Newton é idêntico ao custo da complexidade via análise clássica.

 

 

6 -     Método Paralelo de Interpolação

 

Introdução

 

Os algoritmos seqüências de interpolação em geral possuem complexidade de tempo igual a O(n2). Alguns estudos de pesquisadores [7] [8], tem mostrado avanços na diminuição deste limite mas estes melhoramentos não são muito significativos. Do ponto de vista prático, a complexidade de tempo O(n2) para o problema da interpolação é bastante razoável na resolução dos problemas. Para os problemas de ordem superior tais algoritmos podem não oferecer performance satisfatória. O avanço dos sistemas de computação paralela motivam os estudos no desenvolvido de algoritmos paralelos de interpolação, especialmente para os problemas de ordem superior. 

 

Existem vários algoritmos paralelos de interpolação. Muitos deles utilizam a representação pelo polinômio de Lagrange. Estes algoritmos  possuem a complexidade de tempo O(Logn) e complexidade de espaço O(n2Logn). Para que estes algoritmos possuam uma constante de proporcionalidade razoável são necessárias complexas implementações utilizando DFT (Discrete Fourier Transform) direta e reversa. Existe uma preocupação quanto a estabilidade numérica destes algoritmos [6] ou seja, o fato dos mesmos utilizarem o número elevado de operações faz com que os erros de arredondamento e truncamento devam ser considerados. 

 

O algoritmo paralelo de interpolação apresentado, possui complexidade de tempo O(Logn) e assim fornece um ganho significativo em relação aos tradicionais algoritmos seqüências. Do ponto de vista de estabilidade numérica o algoritmo possui acumulação de erros similares aos algoritmos seqüenciais [6]. A complexidade de espaço deste algoritmo é O(n2).

 

O algoritmo paralelo de interpolação apresentado aqui utiliza a representação de Newton para o polinômio interpolador. Esta representação, conforme veremos mais a frente, utiliza uma expansão das diferenças dividas (DD) como uma combinação linear dos valores da função. Este algoritmo pode ser implementado em arquiteturas com memória compartilhada ou distribuída. Em particular iremos apresentar pseudo códigos para uma arquitetura PRAM CREW (Parallel Random Access Machine  Concurrent Read Exclusive Write).

Algoritmo Paralelo de Interpolação de Newton

 

O polinômio interpolador de Newton é completamente determinado pelos coeficientes das diferenças divididas (DD). Os coeficientes e o polinômio, podem ser escritos como:

 

 

 

 (1)

 

Conforme visto na seção 3, os coeficientes necessários para calcular um polinômio (n=4) são a seguinte tabela triangular:

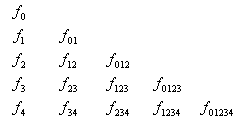 (2)

 

As entradas da diagonal principal são os coeficientes requeridos para o polinômio interpolador de Newton. É interessante observar que os termos de uma dada coluna podem ser calculados independente uns dos outros, porém dependem dos termos da coluna anterior. Assim podemos derivar um algoritmo paralelo trivial para o calculo destes coeficientes utilizando um processador para cada elemento na coluna da tabela. Este algoritmo irá computar os coeficientes das DD’s em O(n) utilizando O(n) processadores.

 

Para podermos diminuirmos o tempo de computação paralelo iremos utilizar uma fórmula alternativa de cálculo das DD’s. Se consideramos:

 

 (3)

 

temos que a  kth DD de f é dada por:

 

 (4)

 

Vamos considerar o inverso do coeficiente  da DD  como sendo:

 

 (5)

 

Assim para calcularmos a kth DD necessária no polinômio de Newton, precisamos computar:

 

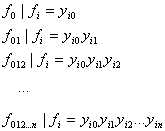 (6)

 

Para calcularmos (6) podemos utilizar o algoritmo paralelo Prefix Sum. Este algoritmo possui a complexidade de tempo igual á O(Logn)  utilizando n processadores [7].

 

A primeira etapa do algoritmo é calcular todos os  necessários para os cálculos das DD’s. Isto pode ser feito em único passo aritmético utilizando (n(n+1))/2 processadores.

 

A segunda etapa é computar através de um Prefix Sum todos os valores de . Na formula (1) devemos aplicar o Prefix Sum n+1 vezes (0 até n referentes a cada termo do somatório), para podermos calcularmos todas as DD’s necessárias. Isto pode ser feita em O(Logn) passos aritméticos concorrentemente utilizando n(n+1) processadores.

 

A terceira etapa é computar as divisões de (4). Para tal utilizamos o resultado da segunda etapa para processarmos as (n x (n+1))/2 divisões necessárias (1). Podemos fazer isto em um único passo aritmético utilizando (n(n+1))/2 processadores.

 

A quarta e última etapa é executar as somas de (4). Isto pode ser feito utilizando o algoritmo paralelo Reduction. Cada soma pode ser feita por este algoritmo em [Log(n+1)] passo aritméticos utilizando n/2 processadores. Novamente como temos n+1 termos no somatório em (1) iremos utilizar ao todo n/2(n+1) processadores.

 

Assim podemos computar todas as DD’s necessárias para o polinômio interpolador de Newton em:

 

2 [Log(n+1)] + 2 passos Aritméticos utilizando n(n+1) processadores  (7)

 

A complexidade de espaço deste algoritmo é dada pela complexidade de espaço necessária para executar os Prefix Sum’s [6]. Isto porque esta etapa do algoritmo é a que consome maior quantidade de espaço. Assim temos que a complexidade de espaço é dado por:

 

4n(n+1)  = O(n2)     (8)

 

Consideração sobre o número de processadores

 

Como vimos em (7) são necessários n(n+1) processadores para a execução do algoritmo apresentado. Vamos considerar que um número limitado de processadores estão disponíveis, em particular quando p= m(n+1) onde 1 < m < n+1 e p é o número total de processadores. Neste caso, nas etapas 2 e 4 iremos distribuir a tarefa de cada um dos (n+1) termos para m processadores. Pode ser mostrado [6] que a complexidade de tempo para o algoritmo para esta situação é dado por:

 

 passo aritméticos  (9)

 

Se possuirmos um número menor que (n+1) processadores disponíveis a aplicação deste método se torna ineficiente [6]. Quando temos m=1 temos O(n) operações no algoritmo, o que nos fornece um speedup de O(n) sobre as implementações seqüências clássicas.

           

 

7 -     Considerações Finais

 

Foi apresentada uma técnica alternativa para calcular o comportamento de determinados algoritmos polinomiais. Dentre os métodos seqüenciais apresentados o método de Newton pode ser considerado uma boa opção, pelo fato de possuir baixa complexidade de computação e não exigir que as abscissas dos pontos a serem utilizados no polinômio interpolador, sejam eqüidistantes.

 

O algoritmo paralelo apresentado se mostra, do ponto de vista teórico, uma boa alternativa para computar os polinômios interpoladores em sistemas de computação de alto desempenho. Gallopoulos [6], mostra um estudo teórico e experimental sobre a estabilidade numérica deste algoritmo. Com os resultados obtidos neste estudo podemos afirmar que o algoritmo paralelo de interpolação de Newton:

 

  1. Produz speedup relevante quando comparado com algoritmos seqüenciais, quando o utilizamos em problemas de ordem superior, n > 70.
  2. Seu resultado de acumulação de erro é similar aos dos algoritmos seqüenciais.

 

Isto torna as implementações do método apresentado rápidas e práticas para problemas de ordem superior.

 

O algoritmo paralelo apresentado assume-se um modelo de computação PRAM CREW no qual os processadores estão totalmente conectados. Pode ser mostrado [8] que a implementação do mesmo em  sistema hiper cubo (cube connected), utiliza apenas 2 passos de roteamento adicionais.

 

 

8 -     Referências Bibliográficas

 

[1] N. Ziviani,  “Projeto de Algoritmos com Implementações em Pascal em C” , 1993

 

[2] F.F. Campos, “Algoritmos Numéricos”, 2001

 

[3] The MathWorks Inc., “MATLAB Reference Guide” Ed. 5.3 , 1999

 

[4] H.T.Kung, “Fast evaluation and interpolation”, 1973

 

[5] E.Horowitz, “A fast method for interpolation using preconditioning” 1972, pp. 157-163

 

[6] E. Gallopoulos, “A Parallel Method for Fast and Practical High-Order Newton Interpolation”1989

 

[7] M.J. Quinn, “Parallel Computing: Theory and Practice”  1994

 

[8] E. Gallopoulos, “A Fast and Practical Parallel Polynomial Interpolation” 1972, pp. 157-163