Abstract
¾ This paper presents a
survey on suffix arrays and their generation. Basic concepts, applications and
three algorithms for parallel generation of suffix arrays are described. The
first algorithm is based on mergesort and the second and the third ones are
based on parallel quicksort. The implementation of the first and second algorithm
are compared on this paper. We show that the second algorithm is more scalable
than the first one and both had speedup. We also show that the speedup is
strongly influenced by network communication latencies.
I. Introdução
Arranjo de sufixos é uma estrutura de dados desenvolvida para pesquisa eficiente em grandes bancos de dados baseados em texto. A estrutura de dados consiste de um arranjo contendo os índices para os sufixos do texto ordenados lexicograficamente. Cada sufixo (sistring) é uma sub-seqüência de caracteres do texto, começando de uma dada posição, e se estendendo até o final do mesmo [1].
A utilização de arranjos de sufixos é mais adequada quando há a necessidade de se manter índices de pesquisa que possibilitem o máximo de eficiência em consultas complexas.
Uma das mais importantes aplicações dos arranjos de sufixos é a pesquisa de seqüências em cadeias de DNA representadas por um texto. Em [2], é apresentado uma aplicação deste tipo, o software STROLL, criado para auxiliar na decodificação do genoma em cadeias de DNA. Outra aplicação interessante de arranjos de sufixos é a identificação de textos plagiados pois é possível verificar a existência de trechos iguais em dois textos.
Os
passos necessários para a construção de um arranjo de sufixos para o exemplo:
ôexemplo de criação de um arranjo de sufixosö serão descritos a seguir.
Índice |
Sufixo |
|
0 |
exemplo
de criação de arranjo de sufixos |
|
8 |
de
criação de arranjo de sufixos |
|
11 |
criação
de arranjo de sufixos |
|
19 |
de
arranjo de sufixos |
|
22 |
arranjo
de sufixos |
|
30 |
de
sufixos |
|
33 |
Sufixos |
Figura 1 û Os
sufixos e seus pontos de indexação
Primeiramente, pontos de
indexação são adicionados ao texto. De acordo com o que foi inicialmente
proposto em [1], cada caractere do texto deveria corresponder a um ponto de
indexação. Por motivos práticos, no exemplo apresentado na Figura 1, cada
palavra corresponde a um ponto de indexação, permitindo que uma pesquisa no arranjo de sufixos seja feita no
início de cada palavra do texto.
Índice |
Sufixo |
|
22 |
arranjo
de sufixos |
|
11 |
criação
de arranjo de sufixos |
|
8 |
de
criação de arranjo de sufixos |
|
30 |
de
sufixos |
|
19 |
de
arranjo de sufixos |
|
0 |
exemplo
de criação de arranjo de sufixos |
|
33 |
Sufixos |
Figura 2 û
Sufixos ordenados lexicograficamente
O segundo passo é a
ordenação dos pontos de indexação lexicograficamente de acordo com seus sufixos
correspondentes. A Figura 2 apresenta o resultado da ordenação lexicográfica
dos pontos de indexação.
Para a realização da busca,
é feita uma pesquisa binária no arranjo de sufixos. Um exemplo de busca no
arranjo de sufixos para a chave æarranjo de sufixosæ é demonstrado na Figura 3.
A setas indicam as etapas da busca binária. O algoritmo de busca gasta O (p log n) tempo para realizar a pesquisa, onde p é o tamanho do padrão n
é o tamanho do arranjo.
|
|
Sufixo |
|
|
2 |
arranjo
de sufixos |
||
|
|
criação
de arranjo de sufixos |
||
|
1 |
de
criação de arranjo de sufixos |
||
|
|
de
sufixos |
||
|
19 |
de
arranjo de sufixos |
||
|
0 |
exemplo
de criação de arranjo de sufixos |
||
|
33 |
Sufixos |
Figura 3 û
Sufixos ordenados lexicograficamente
Um
problema desta estrutura de dados é o tamanho do arquivo resultante que,
normalmente, está entre 120% a 240% do
texto original. Esse fator é crítico durante o processo de busca binária. Para
otimizar o tempo de busca, uma estrutura auxiliar de dados chamada supra-indice [3] é utilizada. Esta
estrutura consiste apenas de uma amostragem de alguns sufixos do arranjo, que
são usados para uma busca preliminar.
Técnicas
de compressão de texto e busca em arranjos de sufixos comprimidos têm sido
usadas por [4] para obter menores arranjos e melhores tempos de busca.
II. geração de arranjos de sufixos
sequencial
No
algoritmo seqüencial, uma única máquina é usada para gerar o arranjo de
sufixos. Esta máquina deve possuir espaço em disco suficiente para armazenar o
arquivo de texto e seu respectivo arranjo de sufixos. Caso o tamanho do texto
seja menor ou igual ao tamanho da memória principal, o problema se resume a uma
ordenação utilizando quicksort. No
caso do texto ser maior que a memória principal, deve-se minimizar o tempo de
busca em disco, utilizando o seguinte algoritmo [3]:
·
Dividir
o texto em blocos do tamanho da memória principal;
·
Ordenar
o primeiro bloco na memória principal;
·
Ordenar
o segundo bloco na memória principal;
·
Intercalar
os dois primeiros blocos ordenados utilizando mergesort;
·
Ordenar
o terceiro bloco na memória principal;
·
Intercalar
o terceiro bloco com arranjo de sufixos já construído;
·
E
assim sucessivamente...
A complexidade deste
algoritmo seqüencial para geração de arranjos de sufixos é O(n2logM/M)
onde n é o tamanho do texto e M o tamanho da memória principal. Esta complexidade demonstra claramente que
uma das principais desvantagens na utilização de arranjos de sufixos, a saber,
é a dificuldade e o custo de construção e manutenção do mesmo, para grandes
bases de texto.
III. geração distribuída de arranjos
de sufixos
Como
alternativa para minimizar o problema do alto custo de construção dos arranjos
foram propostos alguns algoritmos paralelos que são descritos a seguir.
A. Mergesort
distribuído
Um algoritmo apresentado em [7], para geração de arranjo de sufixos paralela, é o mergesort distribuído. Primeiro, o texto
é particionado em Nb blocos de tamanho sblk. Cada bloco
de texto bi é ordenado localmente, usando-se quicksort. Após a geração destes arranjos de sufixos, a máquina i
terá o bloco de texto bi e seu arranjo de sufixos pi
armazenados em sua memória principal. O
próximo passo é realizar a intercalação destes arranjos de sufixos na memória
agregada (sem armazená-los no disco). Já que todos os arranjos estão ordenados, o mergesort é usado para realizar a intercalação distribuída dos
mesmos.
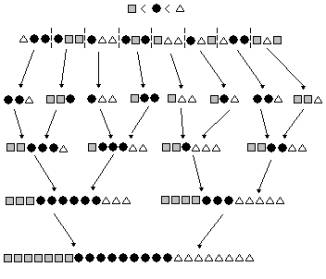
Figura 4 û Exemplo de execução do algoritmo distribuído paralelo mergesort
A Figura 4 demonstra um exemplo do processo de construção do arranjo de sufixos. Na primeira iteração são utilizadas 8 máquinas agrupadas em pares para a intercalação dos arranjos locais. O arranjo de sufixos resultante é então armazenado na memória agregada destas duas máquinas. Na próxima iteração, as máquinas são agrupadas em quáduplas e assim sucessivamente até que na última iteração todas as máquinas estão agrupadas e realizam a intercalação final.
O tempo total de execução do
algoritmo é composto pela soma do tempo
necessário para a ordenação local mais o tempo necessário para a execução do mergesort paralelo (que está fortemente
ligado ao número de mensagens enviadas e à largura de banda disponível). Em [7]
é demonstrado que esse tempo total é:
onde o spkt é o
tamanho do pacote da mensagem e tpkt é o tempo de transmissão do
pacote. Já que T = Nb * Sblk a complexidade do algoritmo
é O(T).
É importante ressaltar que o
algoritmo paralelo não deve utilizar memória secundária, portanto o tamanho de
cada bloco de texto bi é definido com base no tamanho da memória principal disponível em
cada máquina. A memória principal é
dividida em 4 partes, que são usadas para armazenar:
a)
O
bloco resultante do processamento do arranjo de sufixos corrente.
b)
O
arranjo de sufixos que está sendo
intercalado
c)
O
bloco de texto bi
d)
Seu
respectivo arranjo de sufixos
Um ponto negativo em relação
a este algoritmo é a baixa escalabilidade do mesmo, ou seja, ao dobrar-se o
tamanho do texto a ser processado e o número de processadores, o tempo
necessário para indexação cresce.
O algoritmo é também
extremamente sensível à largura de banda, latência e quantidade de memória
disponíveis. Apesar dos aspectos negativos, o mergesort disbribuído apresenta-se como uma alternativa
interessante quando comparado com o algoritmo seqüencial, que é O(n2logM/M), onde n é o tamanho do texto e M é o tamanho
da memória primária disponível.
B.
Algoritmo baseado em quicksort 1
Em [8], é apresentado um
algoritmo paralelo para a construção de arranjos de sufixos distribuído baseado
em quicksort. Neste algoritmo, r processadores devem colaborar para a
construção do arranjo. A análise do custo deste algoritmo é dividida em duas
partes: custo de processamento, indicado pelo fator I e custo de comunicação indicado pelo fator C.
Assumindo que cada um dos r processadores armazena em sua memória
local um bloco com b posições de
texto, o algoritmo pode ser descrito em quatro passos:
·
Passo
1: Cada processador percorre seu texto local, encontrando os pontos de índice
de interesse (geralmente utiliza-se o inicio de palavras); constrói-se então,
um arranjo com todas as posições desses pontos de índice. Os apontadores são
incrementados para refletir suas posições no texto global. Feito isso, o
arranjo é ordenado lexicograficamente em função dos sufixos relacionados aos
pontos de índice. O custo deste passo é O(b
log b) I no caso médio e no pior caso, onde b é o tamanho do bloco.
·
Passo
2: Os r processadores cooperam para estimar os rû1 percentis globais, que definem a porção de cada bloco que será
armazenada em cada processador. Neste passo, cada processador encontra seus percentis locais (pontos de índice que
dividem o arranjo local em r partes
iguais) e os envia para todos os outros processadores. A estimativa dos percentis globais correspondem às
medianas de cada conjunto de percentis
locais ordenado. É importante ressaltar que esta estimativa apresenta um leve
desvio em relação aos valores reais. Neste passo o custo da troca de percentis é da ordem de O(r2) C e o custo de ordenação é O(r2
log r) I.
·
Passo
3: Uma vez que cada processador conhece os r-1
percentis globais, é feito o particionamento dos arranjos de sufixos locais. Em
seguida os processadores realizam a redistribuição para enviar a cada
processador a partição local correspondente. Neste mecanismo de troca, cada
processador formará um par com cada um dos outros processadores em algum
momento, sendo que quando dois processadores formam um par eles trocam
partições dos seu arranjo de sufixos local. É importante lembrar que juntamente
com cada partição os processadores devem enviar o conjunto de sufixos
correspondentes, já que esta informação é necessária para a intercalação dos
pontos de índice. Porém isto tornaria o algoritmo inviável devido ao alto custo
de comunicação. Assim apenas os L primeiros caracteres do sufixo (sufixo
truncado) são enviados, sendo que L deve ser grande o suficiente para evitar um
excesso de mensagens extras de desempate. Neste caso, compressão pode ser usada
para minimizar a quantidade de texto a ser trocada.
·
Passo
4: O passo final corresponde à intercalação das várias partições recebidas já
ordenadas. Porém neste caso os elementos apontados podem corresponder a texto
remoto. Como cada processador recebeu juntamente com os pontos de índice apenas
uma parte de tamanho L do sufixo, alguma comunicação adicional pode ser
necessária para resolver casos onde houver empates.
Na figura 5 podemos ver um
exemplo de construção de um arranjo de sufixos utilizando 3 processadores.
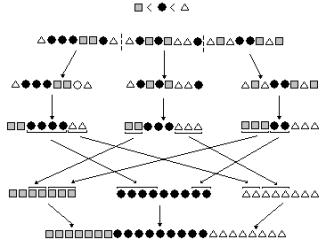
Figura 5 û Exemplo de execução do algoritmo distribuído paralelo quicksort 1
C. Algoritmo baseado em quicksort 2
Outro algoritmo baseado em quicksort é apresentado em [9]. Este
algoritmo inicia com cada processador definindo o início de cada sufixo do seu
bloco do texto e gerando os pontos de índice correspondentes. Deste modo são
formados os arranjos de sufixos locais que são ordenados também localmente em
O(blogb). Os processadores então iniciam um processo recursivo que pode
ser dividido em três partes:
·
Todos
os processadores colaboram para estimar a mediana global (pivô) do arranjo de
sufixos. Para isto cada processador encontra sua mediana local e envia para
todos os outros processadores, o pivô será a mediana do conjunto de medianas
locais, nesta parte temos O(r) C para
distribuir a mediana local entre os processadores e O(r + log b) I para
calcular a mediana global e encontrá-la no arranjo de sufixos local.
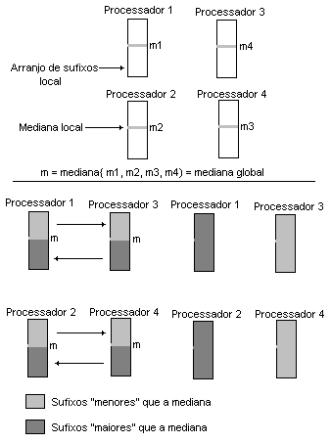
Figura 6 - Exemplo
de construção de arranjos de sufixos com o algoritmo baseado em
quicksort 2
·
Os
processadores se agrupam em pares e trocam partições dos arranjos locais de
modo que em cada par, um dos processadores fique apenas com sufixos
"maiores" que a mediana e o outro apenas com sufixos
"menores" que a mediana. A complexidade deste passo é O(b)C, como o este passo é executado (log r) vezes (devido a recursividade). Assim
temos uma complexidade final de O(b
log r) C.
·
Cada
processador intercala a partição recebida com a sua própria partição, com uma
complexidade final de O(b log r) I. Então este processo reinicia sendo
que, desta vez teremos dois grupos com r/2
processadores trabalhando separadamente (No caso da Figura 6 teríamos um grupo
formado pelos processadroes 1 e 2 e outro grupo formado pelos processadores 3 e
4). Neste passo temos o mesmo problema do algoritmo anterior onde os elementos
apontados podem corresponder a texto remoto, causando trocas de mensagens
adicionais no caso de empates no decorrer da intercalação.
IV. comparação dos algoritmos e
resultados
Para a realização dos experimentos, foi utilizado o código
desenvolvido por [10]. O código foi implementado em linguagem ANSI C no ambiente UNIX para ser executado em um
computador paralelo IBM SP. Para a
exploração do paralelismo foi usada a biblioteca MPI (Message Passing Interface), portanto o
paradigma de programação utilizado é aquele baseado em passagens de mensagens.
O IBM Scalable Power (Performance Optimized With Enhanced RISC), ou SP, é uma máquina paralela MIMD (Multiple Instruction Flow, Multiple Data Flow) de memória distribuída. É constítuída por uma rede de alta velocidade de estações de trabalho utilizando processadores RISC conectados através de um comutador de alto desempenho.
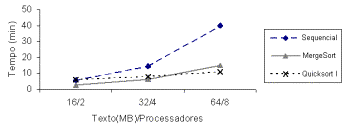Figura 7 ûComparação entre algoritmos de arranjos de sufixos.
O sistema utilizado para a geração dos resultados
apresentados foi IBM 9076 SP do LMC
(Laboratoire De Modélisation et Calcul), situado em Grenoble, na França. Este sistema possui 32 processadores RS-6000 com clock de 66 MHz, 64 MB de memória RAM, 3 GB de disco local com taxa de transferência de pico de 40 MB/s, 64 KB de cache de dados e 8 KB de cache de instruções por nó. Os processadores podem trocar mensagens através de uma rede local de 10 Mbits/s, ou através do HPS de 40 MB/s de pico. O sistema operacional da máquina SP é o AIX 4.2 com PE 2.3.
Na Figura 7 é apresentada uma comparação envolvendo o algoritmo seqüencial e os algoritmos paralelos baseados em mergesort e quicksort 1, sendo que os tempos de execução dos algoritmos foram obtidos de [10] no SP do LMC, com a memória primaria restrita a 32 MB. Todos os algoritmos foram executados com sufixos truncados em 48 caracteres e sem indexação de stop words. Os textos utilizados no experimento correspondem a fragmentos da coleção do WSJ (Wall Street Journal).
Pode-se observar, através da Figura 7, que os algoritmos paralelos apresentam um desempenho melhor que o algoritmo seqüencial, sendo que a escalabilidade do algoritmo paralelo baseado em quicksort 1 é melhor que do algoritmo paralelo baseado em mergesort, pois dobrando-se o tamanho do texto e o número de processadores, o algoritmo baseado em mergesort apresenta uma curva de crescimento para o tempo de execução mais acentuada.
V. Conclusões e trabalhos futuros
Neste
trabalho foram apresentadas algumas propostas para construção de arranjos de
sufixos em paralelo que se mostraram
boas alternativas em relação ao algoritmo seqüencial. O algoritmo mergesort se mostrou pouco escalável,
mas com desempenho superior à implementação seqüencial. O algoritmo quicksort 1, ao contrário mostrou boa
escalabilidade.
Um
fator crítico nos algoritmos paralelos é a latência apresentada pela tecnologia
de rede utilizada, pois existe uma grande troca de mensagens. Este foi o motivo
da escolha de uma máquina paralela, com baixa latência de comunicação para a realização dos testes [10],
Tecnologias atuais, com
baixas latências de comunicação, como por exemplo a GigaBit ethernet vêm se tornando cada vez mais acessíveis. A adaptação dos algoritmos paralelos apresentados para um ambiente de Network of Workstations interconectado
por uma rede GigaBit ethernet possivelmente
também apresentará resultados satisfatórios.
referências
[1] U.
Manber and G. Myers. Suffix arrays: A new method for on-line string searches.
SIAM Journal on Computing, 22, 1993.
[2] T. Chen, S. Skiena. Trie-Based Data
Structures for Sequence Assembly,
Departament of Computer Science, State of New York University, June,
1997.
[3] R. Baeza-Yates, B.
Ribeiro-Neto. Modern
Information Retrieval. Addison Wesley Longman, 1998.
[4] R. Grossi and J. S. Vitter, ``Compressed
Suffix Arrays and Suffix Trees with Applications to Text Indexing and String
Matching'', ACM Symposium on the Theory
of Computing (STOC 2000), Portland, U.S.A. (2000) ACM Press.
[5] S.
Takabayashi. Writing Assistance through Search Techiques. Master´s Thesis, Nara
Institute of Science and Technology, 2001.
[6] M. Cristo et al. Experimental Analysis of a Parallel Quicksort-Based Algorithm for Suffix Array Generation. Departamento de Ciência da Computação, Universidade Federal de Minas Gerais, 1998.
[7] J. P. Kitajima, M. D. Resende, B. Ribeiro, and N. Ziviani. Distributed parallel generation of índices for very large text databases. Technical Report 008/97, Universidade Federal de Minas Gerais û Departamento de Ciência da Computação, Belo Horizonte, Brazil, April 1997.
[8] G.
Navarro, J.P. Kitajima, B. Ribeiro-Neto, N. Ziviani, Distributed Generation of
Suffix Arrays. In A. Apostolico and J. Hein, editors, Proc of the Eighth
Symposium on Combinatorial Pattern Matching (CPM97), Springer-Verlag Lecture
Notes in Computer Science v. 1264, pages 102-115 Arhus, Denmark, June 1997.
[9] G. Navarro, J.P. Kitajima, B. Ribeiro-Neto, N. Ziviani, Distributed Generation of Suffix Arrays a Quicksort-Based Approach. Departamento de Ciência da Computação, Universidade Federal de Minas Gerais, 1997.
[10] M. Cristo. Construção Distribuída de Arranjos de Sufixos com Algoritmos Baseados em Quicksort. Dissertação de Mestrado, Departamento de Ciência da Computação, Universidade Federal de Minas Gerais, 1998.