Fatoração de Inteiros por meio de
Computação Distribuída
Humberto Nigri
Paulo José
Lage Alvarenga
Universidade
Federal de Minas Gerais
Departamento
de Ciência da Computação
Abstract.
Este trabalho tem por objetivo mostrar os esforços já
realizados na busca de algoritmos eficientes para fatoração de números inteiros
e os resultados conhecidos. O enfoque principal está direcionado para as
soluções envolvendo computação paralela e distribuída e para as principais
soluções aplicáveis.
1. Introdução. O problema
em encontrar fatores primos de grandes números compostos sempre foi um
interesse matemático. Com o advento dos sistemas de criptografia baseados em
chave pública, é também de importância prática, porque a segurança de alguns
desses sistemas criptográficos, tais como o sistema Rivest-Shamir-Adelman
(RSA), dependem da dificuldade da fatoração das chaves públicas.
Atualmente é possível fatorar em
tempo hábil números de 100 dígitos na base decimal, e é possível fatorar números de 200 dígitos decimais (512 bits). Este
trabalho descreve alguns dos principais algoritmos de fatoração de inteiros,
considerando sua adaptabilidade para implementação em máquinas paralelas, dando
exemplos da capacidade atual. Em particular, será considerado o problema da
solução paralela de grandes sistemas lineares esparsos, os quais são resultados
da utilização dos métodos MPQS e NFS.
Ainda não é conhecido um algoritmo
determinista ou aleatório em tempo polinomial para encontrar um fator de dado
inteiro composto N. Este fato empírico é de grande interesse, porque o
algoritmo mais popular para criptografia, o RSA, seria inseguro se um algoritmo
rápido para fatoração de inteiros pudesse ser implementado.
1.1. Algoritmos aleatórios. Todos
algoritmos, com exceção dos mais triviais, são algoritmos aleatórios. Em algum
ponto eles envolvem escolhas pseudo-aleatórias. Por isso os tempos de execução
são esperados menores que o pior caso. No entanto, na maioria dos casos
esperados, o tempo de execução é uma conjectura, e não foi rigorosamente
provado.
1.2. Algoritmos paralelos. Quando
algoritmos paralelos são projetados, é esperado que o algoritmo que requer
tempo T1 em um computador com um processador possa ser implementado
para executar em tempo TP ≈ T1/P
em um computador com P processadores independentes. Este nem sempre é o caso,
pois pode ser impossível utilizar todos os P processadores efetivamente. No
entanto, isso é realidade para muitos algoritmos de fatoração de inteiros,
desde que P não seja muito grande.
O Speedup
de um algoritmo paralelo é S = T1/TP.
O objetivo é um speedup linear, por exemplo S =
Θ(P).
1.3 Algoritmos quânticos. Em 1994 Shor mostrou que é possível fatorar
em um tempo polinomial esperado, em um computador quântico. No entanto, apesar
dos melhores esforços de vários grupos de pesquisa, tal computador ainda não
foi construído, e ainda é incerto quando será perceptível a construção de um.
Por isso a atenção será dada apenas a algoritmos os quais são executados em
computadores clássicos (seriais ou paralelos).
1.4 Lei de Moore.
A “Lei” de Moore prediz que a densidade de
circuitos duplicara a cada 18 meses ou menos. É claro que a Lei de Moore não é um teorema, e poderá eventualmente falhar, mas
ela foi surpreendentemente precisa por muitos anos. Enquanto a Lei de Moore continuar adequada e resultar em correspondentemente
computadores paralelos mais poderosos, é esperado obter uma grande melhoria na
capacidade dos algoritmos de fatoração, sem qualquer melhoria algorítmica.
Historicamente, melhorias acerca
dos últimos 30 anos foram devidas à lei de Moore e ao
desenvolvimento de novos algoritmos, como ECM, MPQS e NFS.
2. Algoritmos de Fatoração de
Inteiros. Existem muitos algoritmos para encontrar um fator
não-trivial f de um inteiro composto N. Os algoritmos mais úteis são inseridos
em uma dessas duas classes:
A.
O tempo de execução depende principalmente do tamanho
de N, e não depende fortemente do tamanho de f. Exemplos são:
q O
algoritmo de Lehman, cujo pior-caso de execução é 
.
q Os
algoritmos Continued Fraction
e Multiple Polynomial Quadratic Sieve (MPQS), dos quais
é plausível assumir um tempo de execução esperado 
, onde 
é uma constante
(dependendo de detalhes do algoritmo). Para MPQS, 
.
q O
algoritmo Number Field Sieve (NFS), do qual é plausível assumir um tempo de
execução esperado 
, onde é uma constante
(dependendo de detalhes do algoritmo).
B.
O tempo de execução depende principalmente do tamanho
de f, o fator encontrado. (Pode-se assumir que 
.) Exemplos são:
q O
algoritmo Curva Elíptica (ECM), de Lenstra, do qual é
plausível assumir um tempo de execução esperado 
, onde 
é uma constante.
Nos exemplos, os limites de tempo
são para máquinas seqüenciais, e o termo 
é uma permissão
generosa para o custo de operação aritmética em números que são O(N²). Se N é
muito grande, então algoritmos rápidos de multiplicação de inteiros podem ser
usados para reduzir o termo.
3 Método da
Curva Elíptica. O método (ou algoritmo) de curva elíptica (abreviado
ECM) foi descoberto por H. W. Lenstra Jr, em cerca de
1985. É o algoritmo mais conhecido da classe B.
Seu funcionamento é da seguinte
forma: dado um inteiro N a ser fatorado, seleciona-se aleatoriamente uma curva elíptica
modulo N e um ponto x no grupo de pontos dessa curva
elíptica.
Primeiro estágio: Seleciona-se um inteiro m1 e eleva-se x para a potência k, onde k é o produto de
todas as potências primas ≤ m1. Se essa computação falhar porque um fator
não-trivial foi encontrado, então termina. Caso contrário, continua com o
segundo estágio.
Segundo estágio: Seleciona-se um inteiro m2 > m1 e
tenta-se computar xkq
para os primos q entre m1
e m2,
sucessivamente. Se a computação falhar é porque um fator não-trivial foi
encontrado, e termina. Senão recomeça todo o processo.
3.1 Implementação paralela ou
distribuída do ECM. ECM consiste de um número de caminhos
pseudo-aleatórios independentes, cada qual podendo ser executado em um
processador separado. Desde que o número esperado de caminhos seja muito maior
que o número de processadores P disponíveis, o speedup
linear é possível executando P caminhos em paralelo. De fato, se T1
é o tempo de execução esperado em um processador, então o tempo de execução
esperado em uma máquina paralela MIMD com P processadores é 
4. Algoritmo Multiple
Polynomial Quadratic Sieve (MPQS). Algoritmos quadratic
sieve pertencem a uma vasta classe de algoritmos que
tentam encontrar dois inteiros x e y tal que x≠±y(mod N) mas
.
Uma vez que cada x e y
são encontrados, então MDC(x-y,N)
é um fator não-trivial de N. Uma
maneira de encontrar x e y satisfazendo as condições citadas é
encontrar um conjunto de relações na forma 
, onde o wi possui todos os fatores primos em um conjunto
moderadamente pequeno de primos (chamado base de fatores). Assim que tenha sido
gerada uma quantidade suficiente de colunas, podemos utilizar a eliminação
Gaussiana em GF(2) para encontrar a dependência linear
(mod 2) entre um conjunto de colunas de R.
Multiplicando as relações correspondentes obtemos uma expressão na forma (2).
Com probabilidade de no mínimo ½ , temos x≠±y mod
N, e desse modo um fator não trivial de N
será encontrado. Se não, é necessário obter uma nova dependência linear e
tentar novamente.
O melhor algoritmo dentre os quadratic sieve é o MPQS, que
difere do primeiro apenas por tentar várias funções y para cada x, e portanto é possível obter vários pares (x,y) antes que |x|
cresça muito.
Podemos assumir plausivelmente que
o tempo de execução do MPQS é da ordem de 
, onde . As constantes envolvidas são tais que o MPQS é usualmente
mais rápido que o ECM se N é o
produto de dois primos, e ambos excedem 
. Isso acontece porque o loop
interno do MPQs envolve
apenas operações com precisão simples, e é da forma:
enquanto j < limite faça
início
s[j] ß s[j] + c;
j ß j + q;
fim
4.1 – Distribuição paralela da
implementação do MPQS. O estágio de peneiração (sieving)
do MPQS é apropriadamente aplicável em implementações paralelas. Diferentes
processadores podem utilizar diferentes polinômios, ou peneirar diferentes
intervalos com o mesmo polinômio. Por isso existe um speedup
linear desde que o número de processadores não seja muito maior que o tamanho
da base do fator.
A computação requer pouquíssima
comunicação entre os processos. Cada processador consegue gerar relações e
encaminhá-las a algum ponto central de coleta. Isso foi demonstrado por A. K. Lenstra e M. S. Manasse[//], que
distribuíram seu programa e coletaram relações através de correio eletrônico.
Os processadores foram espalhados ao redor do mundo – qualquer
pessoa com acesso a um correio eletrônico e a um compilador C poderia tornar-se
voluntário e contribuir.
O estágio final do MPQS –
Eliminação Gaussiana para combinar as relações – não é tão facilmente
distribuído, pois requer muita comunicação entre os processadores. Por isso,
geralmente esta etapa é executada em um super-computador
não paralelo.
Porém isso não se torna crítico ao
algoritmo, pois apesar de exigir uma taxa alta de processamento, a grande
proporção de processamento já foi feita paralelamente, anteriormente.
5. Number Field Sieve (NFS). O algoritmo General Number Field Sieve
(GNFS), ou simplesmente Number Field
Sieve (NFS) foi desenvolvido com base em outro
algoritmo, chamado Special Number
Field Sieve (SNFS). Para
melhor entendimento do NFS, será abordado, a princípio, o funcionamento do
SNFS.
A maioria dos exemplos numéricos
envolve números na forma:
ae±b,
para pequenos a e b, no entanto o ECM e o MPQS não tira vantagem dessa forma
especial.
O SNFS é um algoritmo
relativamente novo que tira vantagem dessa forma especial. Em seu conceito, ele
é similar aos algoritmos QS, mas ele trabalha sobre um campo numérico algébrico
definido por a, e e b.
O NFS é uma extensão lógica do
SNFS. Quando usamos SNFS para fatorar um inteiro N, nós necessitamos de dois polinômios f(x)
e g(x) com uma raiz em comum m
mod N mas sem raiz comum sobre o campo de números complexos. Se N possui a forma especial, então é
usualmente fácil escrever polinômios adequados com coeficientes pequenos.
Supondo que g(x) possui grau d > 1 e f(x) é linear, d é escolhido empiricamente, mas são
conhecidas de considerações teóricas que o valor ótimo é 
.
Escolhe-se m = 
e escreve-se 
, onde aj
são “dígitos base m”. Então, definindo 
, 
, é claro que f(x) e g(x) possuem raiz comum m mod N. Este método de seleção polinomial é
chamado método “base m”.
Em princípio é possível prosseguir
como no SNFS, mas existem muitas dificuldades decorrentes dos grandes
coeficientes de g(x). Porém essas dificuldades foram
ultrapassadas é possível utilizar esse método na prática. Devido a fatores
constantes envolvidos, ele é mais lento que o MPQS para números de menos que
cerca de 110 dígitos decimais, mas é mais rápido que o MPQS para números
suficientemente grandes, como previsto na teoria.
Algumas das dificuldades que
tiveram que ser ultrapassadas para transformar o GNFS em um algoritmo prático
são:
- Seleção polinomial. O método “base m” não é
muito bom. Peter Montgomery e Brian Murphy mostraram como uma melhoria muito considerável
(por um fator de mais de dez para números de 140-155 dígitos) pôde ser
obtida.
- Álgebra Linear. Após a peneiração, um sistema
linear esparso através do GF(2) é obtido, e é
necessário encontrar as dependências entre as colunas. Não é prático
executar essa tarefa através da eliminação Gaussiana estruturada, porque a
matriz compacta é muito grande. Odlyzko e
Montgomery mostraram que o método Lanczos
poderia ser adaptado para este propósito. Para tirar proveito do
paralelismo de bits nas operações, o programa de Montgomery trabalha com
blocos de tamanho dependente da palavra de máquina (por exemplo, 32).
- Raízes quadradas. O estágio final do GNFS
envolve encontrar raízes quadradas de um produto algébrico (muito grande)
de números, e mais uma vez Montgomery encontrou uma forma de ultrapassar o
problema.
5.1 Distribuição Paralela do NFS. O estágio de peneiração (sieving) é similar ao
do MPQS, sendo, também, facilmente paralelizável. As dificuldades da
paralelização do NFS serão discutidas a seguir.
6. Paralelismo da Álgebra Linear. No
presente, o principal obstáculo para uma implementação totalmente paralela e
escalar do GNFS (e, em menores extensões, MPQS) é a álgebra linear.
O programa de Lanczos
com blocos de Montgomery é executado em um processador simples e requer memória
suficiente para armazenar a matriz esparsa (cerca de cinco bytes por elemento
diferente de zero). É possível distribuir a solução de Lanczos
com blocos por vários processadores de uma máquina paralela, mas a taxa de
comunicação/computação é muito alta.
Além disso, existe uma série de
requisitos para conseguir paralisar esta etapa do algoritmo, como, por exemplo,
para melhorar a comunicação, haveria a necessidade de se organizar os
computadores de uma forma quadrática (por exemplo, 16 ou 64 computadores
interligados), em uma topologia grid ou torus, de modo que um processador poderia comunicar com
outros da mesma linha sem interferir na comunicação que está sendo feita em
outras linhas, sendo similar para as colunas. O não uso dessa topologia
penalizaria a comunicação de modo que o fator seria multiplicado pela ordem 
. Uma das sugestões feitas por Brent [4] é realizar uma
eliminação Gaussiana para eliminar os maiores primos e suas k relações,
diminuindo, assim, a quantidade de trocas na comunicação entre os
processadores. Porém, apesar de melhorar a comunicação, haverá maiores
necessidades de armazenamento da matriz esparsa gerada, assim como um
crescimento de seu peso total.
7. Uso do processamento paralelo.
Devido à facilidade de se dividir a parte algorítmica de maior custo
entre vários computadores com baixa taxa de comunicação tornou viável a distribuição
em massa dos dados via Internet. A primeira proposta encontrada sobre o assunto
é de Lenstra, data de 1989, e consistia em distribuir
tarefas a vários computadores ao redor do mundo, necessitando somente de um
compilador C e de acesso a um correio eletrônico. Um servidor coletaria dados
dos processos distantes (que chegariam por correio eletrônico), e outro
trataria a informação. Os resultados levaram a fatorar
números com mais de 30 dígitos em menos de 1 dia, e
números com 100 dígitos em cerca de um mês com a distribuição paralela em 1200 PCs
da IBM e o algoritmo MPQS.
Um projeto foi realizado por Brent [1] em 2000, e obteve
resultados significativos. Este projeto complementou a Tabela de Cunningham, com as bases entre 13 e 99. Os métodos
utilizados foram o ECM para encontrar fatores de até 30 dígitos, e depois de
encontrados esses fatores, foram utilizados o MPQS e o NFS para encontrar os
fatores maiores. Os valores encontrados (que preenchem aproximadamente 500
páginas) podem ser visualizados em [1].
Atualmente existe um grupo chamado NSFNET [7] que também
tira proveito do uso de computação gratuita, distribuindo processos entre
computadores de voluntários através da Internet. Esse grupo apresentou como seu
resultado mais recente (6 de junho de 2004) o fato de
ter fatorado o número conhecido como M811, ou seja, 2811-1, um número de 239 dígitos,
que foi fatorado em 3 prováveis primos, de 83, 63 e
92 dígitos, na ordem de sua descoberta. Segundo eles, foram usadas mais de 15.000
horas de processamento em processadores Pentium III, apenas para a etapa da
Álgebra Linear (que teve que ser rodada duas vezes, pois a primeira, não obteve
sucesso). O resultado final levou mais de dois meses de computação sólida em um
cluster de 30 CPUs, sendo
que dois terços dessa computação foi desperdiçada.
Portanto, apesar de ter menor custo que o processo de “sieving”, esse custo não deixa de ser muito alto, e isso
tem gerado pesquisa e investimento a fim de possibilitar um paralelismo total
do algoritmo NFS com custo de comunicação reduzida e facilidade de distribuição
através da Internet.
8. Conclusões. Foram
analisados os três principais algoritmos de fatoração de inteiros no momento:
ECM, MPQS e GNFS, assim como as dificuldades de executar cada algoritmo em
computação paralela.
Analisando historicamente os
resultados dos algoritmos, nota-se que foi feito um progresso significante na
última década. Isso é devido parte à Lei de Moore,
parte à melhoria de técnicas de paralelismo, juntamente com a facilidade de seu
uso através da Internet e parte devido às melhorias nos algoritmos
(especialmente GNFS).
O maior número fatorado
pelo MPQS em 1990 possuía “apenas” 111 dígitos decimais. Em 1994 o RSA129 foi fatorado pelo MPQS. Em 1996, GNFS ultrapassou o MPQS, fatorando RSA130. Em 1999, RSA155 também foi fatorado pelo GNFS. Dados obtidos do NFSNET group indicaram ter fatorado, em
6 de junho de 2004, o M811 (possui 239 dígitos decimais, e corresponde ao
número 2811-1). Na figura 1 pode-se verificar o crescimento da
quantidade de dígitos dos números fatorados até o ano
2000.
A melhor metodologia aparente para
fatoração de inteiros atualmente foi utilizada por Brent [1], e constitui em um
refinamento sucessivo de uso dos três algoritmos. Utiliza-se primeiramente o
ECM, para encontrar os fatores menores que 30 dígitos, e posteriormente são
utilizados, paralelamente, o MPQS e o GNFS, para encontrar os fatores maiores.
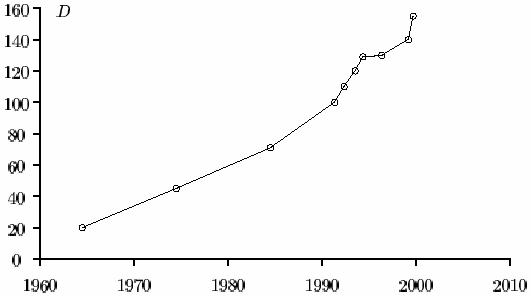
Figura 1: Crescimento da quantidade de dígitos dos números fatorados até o ano 2000
Não há previsão de grandes
descobertas de algoritmos nos próximos anos, porém, de acordo com a Lei de Moore, há previsão de que os algoritmos continuarão aumentando
em uma taxa de cerca de 3 a 4 dígitos por ano. No
entanto, O número de 239 dígitos com primos próximos mostrou que esse crescimento
está sendo maior que o esperado.
Quanto à finalidade dos algoritmos
de fatoração, já é possível dizer que o RSA de 512 bits é inseguro, e o RSA de
1024 bits já é alvo almejado dos algoritmos de fatoração de inteiros. O que está sendo proposto para garantir
segurança é a utilização de chaves com o tamanho de 2048 bits.
A facilidade de se obter um speedup próximo do linear com os algoritmos propostos é um
dos fatores que viabiliza a fatoração de números maiores, porém essa facilidade
se tornaria desnecessária se fosse descoberto um computador quântico capaz de
executar o algoritmo citado no capítulo 1.3. Como não existe previsão da
descoberta de tal computador, os algoritmos paralelos são a melhor opção
prática, e estes ainda não oferecem risco imediato à segurança da criptografia
com chave de 2048 bits do RSA.
9. Bibliografia
[1] Richard P. Brent, Peter L.
Montgomery and Herman J.J.
te Riele, Factorizations of Cunningham Numbers with bases 12 to 99: Millennium Edition, PGR-TR-14-00, 2000
[2] Richard P. Brent, Integer Factorization,Grand Challenges
in Supercomputing at the Australian National University pgs. 34-39, Canberra,
ACT 0200, 1994
[3] Richard P. Brent, Some Parallel Algorithms for Integer Factorisation, Euro-Par’99,
Toulouse.
[4] Richard P. Brent, Recent Progress and Prospects for integer factorisation algorithms, PRG-TR-03-00, 2000
[5] Arjen
K. Lenstra, Mark S.
Manasse, Factoring by eletronic mail, 1989
[6] Peter L. Montgomery, A survey of Modern Integer Factorization Algorithms, CWI
Quarterly, Volume 7 (4)
1994, pp. 337-365
[7] NFSNET – Large-scale
Distributed Factoring,
disponível em 28/06/2004, no endereço http://www.nfsnet.org