Universidade Federal de Minas Gerais
Instituto de Ciências Exatas
Departamento de Ciência da Computação
Algoritmos e Estruturas de Dados I
Estruturas & comandos para controle do fluxo de execução
Seqüência
Na linguagem C o fluxo de controle passa sequencialmente de um comando para o seguinte na ordem convencional de leitura. Este é o tipo de estruturação mais simples do fluxo de controle e é denominado seqüência. Considere o seguinte trecho de programa:
int a=2;
int b=3;
int c=4;
Quando o fluxo de controle atinge a sentença int a=2; ocorre sua execução, em seguida ou na seqüência o fluxo de controle se dirige para a sentença int b=3; e ocorre sua execução e na seqüência o fluxo de execução atinge a sentença int c=4; Este não é um bom exemplo porque envolve sentenças de definição/declaração de variáveis e isto pode envolver aspectos não sequenciais. O exemplo abaixo é melhor porque envolve apenas comandos de atribuição e a linguagem dá garantias de execução sequencial. Quando o fluxo de controle atinge o comando de atribuição a=2; a expressão é avaliada (avaliação da constante 2 resultando no valor 2) e em seguida é feita a atribuição do valor 2 à variavel a. Isto ocorre de maneira similar para os dois comandos de atribuição seguintes (em sequência).
a=2;
b=3;
c=4;
Blocos
Na linguagem C podemos agrupar uma seqüência de sentenças ou comandos através do uso de abre e fecha chaves - {}. Os comandos assim agrupados passam a formar o que é denominado um bloco. Quando o fluxo de controle atinge um bloco cada um dos comandos que formam o bloco são executados em seqüência. O uso de blocos é especialmente importante no caso de comandos condicionais e iterativos. Mas. além disso, será visto que blocos estabelecem um escopo para variáveis.
Comando se-então-senão
Nas linguagens de alto-nível existem vários tipos de comandos denominados
comandos condicionais que permitem ao programador expressar que, em função do
resultado de uma expressão, ele quer que o fluxo de controle vá para diferentes
grupos de comandos. Na linguagem C um destes comandos é o comando if. O comando if tem a seguinte
forma:
if(<expressão> ) <comando1>; else <comando2>;
Quando o fluxo de controle atinge o comando if:
- a <expressão> é avaliada (deve ser um tipo compatível com operador !=).
- se a <expressão> resultar no valor true (valor diferente de zero) o fluxo de controle vai para o <comando1> e após a execução do <comando1> o fluxo de controle deixa o comando if.
- se a <expressão> resultar no valor false (valor igual a zero) o fluxo de controle vai
- para o <comando2> e após a execução do <comando2> o fluxo de controle deixa o comando if.
Ou seja, dependendo do valor da <expressão> , o fluxo de controle irá para <comando1> ou <comando2
de forma mutuamente exclusiva.
Abaixo são mostradas algumas formas do comando if:
if(<expressão>) <comando1>; /* não tem a
cláusula else */
A cláusula else
é opcional. Quando o fluxo de controle atinge um comando if que não contém a clausula else,
o fluxo de controle passa para a avaliação da expressão. Se o resultado final
da avaliação da expressão for (diferente de zero) true
o fluxo de controle passa para o <comando1> e após a execução do
<comando1> o fluxo de controle deixa o comando if. Se a expressão for (zero) false o fluxo de
controle deixa o comando if
e o único efeito foi a avaliação da expressão.
if(<expressão>) { <c1>; <c2>;
<c3>;} /* uso do bloco */
Quando queremos executar vários comandos juntos ao “então” ou vários comandos
juntos ao “senão” temos que usar o bloco - {}, para agrupá-los.
A seguir exemplificamos com alguns trechos de programa o uso do comando
se-então-senão na linguagem C
Obter o valor absoluto da variável x:
if(x<0) valorAbsoluto=-x; else valorAbsoluto=x;
(equivale a valorAbsoluto= x<0 ? -x : x; )
Obter o maior valor entre x e y:
if(x>y) maior=x; else maior=y; /ou
if(x<=y) maior=y; else maior=x;
A forma de escrever uma decisão com múltiplos caminhos é:
if(<expressao1>)
<comando1>;
else if(expressao2>)
<comando2>;
else if(expressao3>)
..<coimando3>;
else
<comando4>
Existe um problema de ambiguidade do “else” quando existe um aninhamento de if’s (um comando if aparecendo na parte então ou senão de um outro if). A .linguagem C define que o else deve ser associado ao “if-sem-else” mais próximo. Não adianta o programador querer “forçar” a associação de if&else através de indentação!
if(<expressao1>)
if(<expressao2>)
printf(“então
aninhado\n”);
else
//indentação com defeito
printf(“else de quem?\n”);
O trecho acima sem “defeito”:
if(<expressao1>)
if(<expressao2>)
printf(“então
aninhado\n”);
else
printf(“else de quem?\n”);
Ainda em relação ao trecho acima, se desejarmos associar o “else” ao primeiro “if”, temos que usar chaves. É uma boa prática usar chaves mesmo que redundantes!
if(<expressao1>){
if(<expressao2>)
printf(“então
aninhado\n”);
}
else
printf(“else de quem?\n”);
Os trechos acima evidenciam que o ponto-e-vírgula (;) tem um carater na linguagem C de “término”. Se for colocado um ponto-e-vírgula após o bloco (após o fecha chaves) então definimos o “término” do comando condicional e não pode haver associação de “else’s”
O tipo da expressão que aparece entre parênteses no comando if .pode ser qualquer tipo (double, int, “endereço”, ...) que aceita o operador !=.:
Podemos usar variáveis ou expressões aritméticas como se fossem variáveis “lógicas” ou variáveis “booleanas”, apesar de não existir o tipo lógico em C, basta lembrar a convenção de que valores diferentes de zero correspondem a “verdadeiro” e valores iguais a z” e valores iguais a zero correspondem a “falso”:
if(N%2==0) printf(“%d e’ par\n”, N);
ou
if(N%2);else printf(“%d
e’ par\n”,N);
ou ainda
int numeroPar;
numeroPar=N%2==0;
if(numeroPar) printf(“%d e’par\n”, N);
Comando escolha
Uma possível forma de generalização do comando se-então-senão é o
comando escolha. Podemos pensar no comando se-então-senão como
sendo um comando que tem uma expressão e que tem um comando associado ao valor
(diferente de zero) verdadeiro e um comando associado ao valor (zero) falso.
Quando a expressão é avaliada será executado o comando associado ao valor
resultante. No comando escolha temos uma expressão do tipo inteiro e
temos vários comandos associados a rótulos que correspondem a constantes inteiras.
O comando escolha na Linguagem C corresponde ao comando switch. O
comando switch permite a transferência do fluxo de controle para um de
vários pontos rotulados com uma constante inteira. A forma geral do comando é:
switch (<expressão>) {
case <constante1>:
<seqüência de comandos1>
case <constante2>:
<seqüência de comandos2>
...
case <contanteN>:
<seqüência de comandosN>
default: <seqüência de comandos default>
}
Quando o fluxo de controle atinge o comando switch:
1. a expressão do tipo int é avaliada
2. o fluxo de controle passa para o comando rotulado com um valor correspondente ao resultado da expressão avaliada. Caso não exista uma constante com rótulo correspondente ao valor da expressão o fluxo de controle é desviado para o comando rotulado com a palavra chave default.
3. o fluxo de controle passa a percorrer os comandos dentro do bloco de forma sequencial e quando o controle atinge o final do bloco o fluxo de controle deixa o comando switch. O fluxo de controle deixa o comando switch quando não existe rótulo com o valor da expressão inteira e também sem o rótulo default.
A parte do comando switch entre abre e fecha chaves é conhecida como bloco do switch. O bloco do switch pode ter comandos que sejam prefixados com rótulos prefixados com a palavra chave case. Quando o fluxo de controle atinge o comando switch a <expressão> é avaliada e o fluxo de controle será desviado para a seqüência de comandos cuja constante do rótulo case tenha o mesmo valor da <expressão>. O fluxo de controle continua ao longo de todo os comandos a partir deste ponto, incluindo as outras seqüências de comandos. Se não existir um rótulo case com uma constante que pareie (faça par, seja igual) ao resultado da <expressão> o fluxo de controle será desviado para a seqüência de comandos com rótulo default. O rótulo default é opcional no bloco do switch e caso o resultado da <expressão> não tenha um rótulo case com contante que o pareie e não exista um rótulo default, todo o comando switch é saltado e o único resultado terá sido a avaliação da <expressão>.
Trecho de programa exemplificando um comando switch em C:
switch (a+b)
{
case 1: printf("1\n");
case 2: printf("2\n");
default: printf("outro\n");
}
Se o resultado de a+b for 1 serão impressas as três
cadeias de caracteres: 1, 2, outro.
Se quisermos que cada seqüência de comandos de cada
rótulo seja excutada de forma mutuamente exclusiva
temos que usar o comando break. O comando break faz o fluxo de controle
se dirigir para o comando seguinte ao switch. Veja o trecho de programa
C abaixo:
switch (a+b)
{
case 1:
printf("1\n");
break;
case 2:
printf("2\n");
break;
default:
printf("outro\n");
}
Comando enquanto e faça-enquanto
O comando enquanto é um dos denominados comandos iterativos ou comandos
de repetição ou ainda simplesmente um laço.
Os comandos iterativos prendem o fluxo de controle e permitem repetir a
execução de comandos. Um comando enquanto tem associado a ele uma
expressão (que segue as mesmas convenções da expressão do comando if) e um comando (que pode
corresponder a um bloco). Quando o fluxo de controle atinge o enquanto a
expressão é avaliada e caso ela seja verdadeira o fluxo de controle será
transferido para o comando associado ao enquanto. Ao terminar a execução
do comando o fluxo de controle retorna para o inicio do comando enquanto,
repetindo a avaliação da expressão e desviando o fluxo de controle para a
execução do comando caso a expressão seja verdadeira. Esta repetição continua
até que a avaliação da expressão dê resultado falso. Somente quando o resultado
da expressão é falso é que o fluxo de controle deixa o comando enquanto
e se dirige para o comando seguinte (ou seja o comando
na “seqüência”).
A forma geral do enquanto (while) na
linguagem C é :
while(<expressão>) <comando>;
Temos que usar bloco - {} - para associar uma seqüência
de comandos ao comando while.
Uma forma alternativa do comando enquanto é denominada faça-enquanto
(do-while):
do <comando> while(<expressão>);
No comando faça-enquanto o comando é executado pelo menos uma vez, no
caso do comando enquanto se a expressão for falsa o comando não é executado nem
uma vez.
Comando para (“for”)
Um comando para tem associado a ele três expressões e um comando. O
comando para é mais um dos comandos iterativos ou comandos de repetiçao. Considere a seguinte forma geral do comando para
(for) na linguagem C:
for(<expressao1> ; <expressao2> ;
<expressao3>) <comando>;
Podemos explicar a semântica deste comando utilizando o comando while. O comando acima tem o mesmo efeito do trecho
de programa abaixo:
<expressao1>;
while (<expressao2>) {
<comando>;
<expressao3>;
}
A <expressao1> também é referida como iniciação; A <expressao2> será avaliada e se for 0 é falsa e se for diferente de 0 é verdadeira. A <expressao3> também é referida como atualização. Existem outras opções sintáticas para o comando for.
Exemplos:
for(i=0; i<20; i++) printf(“*”);
//o código de iniciação tem uma atribuição e o código de atualização tem uma
atribuição(incremento)
for(i=0, j=1; i!=j; ){ ... }; // o código de iniciação tem duas atribuições e o código de atualização esta ausente.
Um programa pode ficar com o fluxo de controle preso em um comando de
iteração, o comando
while(TRUE);
Equivale ao comando
for(;;);
e corresponde a prender o fluxo de controle sem previsão explícita de saída do
controle. Observe que os itens 1 2 e 3 do comando for são opcionais, e a
ausência do <expressao2> faz o compilador interpretar o comando como
sendo
for(;TRUE;);
---
O entendimento de um trecho de programa contendo comandos de iteração (fluxo de execução laçado!) não é uma tarefa simples. O âmago de vários diferentes paradigmas de linguagens de programação é substituir a iteração por outros tipos de construções. Existem várias maneiras de compreender ou entender uma iteração sendo que algumas são aplicáveis em alguns casos e outras não. O chamado “desdobramento de um laço” muitas vezes ajuda no entendimento inicial na leitura de programas. Não vamos mostrar um tratamento sistemático deste assunto e ao invés disso vamos mostrar alguns exemplos simples.
Considere o seguinte trecho de programa:
for(i=0;
i<3; i++) printf(“%d\n”,i);
este trecho pode ser “substituido” por este trecho:
printf(“%d\n”,0);
printf(“%d\n”,1);
printf(“%d\n”,2);
A substituição de um comando de iteração pelos comandos que ele itera é denominado “desdobramento da iteração”. Agora considere este outro trecho:
int n;
scanf(“%d”, &n);
for(int i=0; i<n; i++) printf(“%d\n”,i);
este trecho pode ser substituído por estre trecho:
printf(“%d\n”,0);
printf(“%d\n”,1);
printf(“%d\n”,2);
...
printf(“%d\n”,n-1);
Agora foi necessário usar “o poder da reticência”. Em algumas especificações de iteração torna-se ainda mais difícil o entendimento do significado, mas a técnica do “desdobramento” é uma importante ferramenta mental para entendimento dos laços. A execução repetida de comandos, além da iteração, pode ser feita, também, utilizando a “Recursão”, conforme será visto mais à frente na disciplina. Um outro mecanismo de entendimento e até mesmo desenho da iteração utiliza três expressões lógicas: (i) uma expressão de pré-condição, (ii) uma expressão de invariante e (iii) uma expressão de pós-condição. Repetindo o que foi dito acima o entendimento de iterações não é um processo simples e exige bastante treino. Os exercícios abaixo pedindo para escrever asteriscos que formam desenhos de figuras geométricas são muito importantes!
A linguagem C possui um comando de desvio do fluxo de
execução similar ao “vá para” do Computador Simplificado. A identificação do
ponto de desvio é feito através de um identificador
denominado rótulo (label). O comando de desvio é o
“goto <rótulo>” e o <rótulo> deve ser definido usando um
identificador seguido de dois pontos. O uso do comando “goto” é considerado um
ato de agressão à legibilidade do programa e portanto
só é respeitado se o programador for experiente e souber justificar o uso. Kernighan e Ritchie consideram que uma situação
justificável é quando é necessário abandonar o fluxo de controle que mergulhou
muito em aninhamentos de laços definidos por “for” e
“while”, exemplo:
for( bla bla bla)
for (bla bla bla)
for(bla
bla bla){
bla bla bla
if(desastre)
goto saiDoAninhamento;
bla bla bla
saiDoAninhamento:
<fluxo continua sequencialmente>
O goto tem restrições relacionadas ao escopo e não é permitido, por exemplo, usar um goto entre diferentes funções. Antes de usar o goto o programador deve verificar se o uso de “break” (que faz o fluxo de controle abandonar o switch ou laço mais interno e executar o próximo comando na sequência) ou o uso de “continue” (que faz o fluxo de controle tomar a próxima iteração do laço mais interno) são mais adequados.
---
Exemplo de uso de “iteração” em um cálculo numérico.
O Programa abaixo calcula um valor aproximado de e, base dos logaritmos
naturais ou neperianos, utilizando a expressão:
![]()
Podemos ler a expressão acima da seguinte forma: o número e corresponde ao somatório do inverso do fatorial de todos os números naturais. Não precisamos somar (nem conseguiriamos) o inverso do fatorial de todos os naturais, os primeiros 10 a 20 termos esgotam a precisão do tipo double.
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[])
{
int
n=1;
double eAtual, eProx=1.0, f=1.0;
do{
eAtual=eProx;
f=f*n;
eProx=eProx+1.0/f;
n++;
}while(fabs(eProx-eAtual)>1.0e-10);
printf("Com
%d iteracoes obteve e=%.10f\n", n, eProx);
system("PAUSE");
return 0;
}
---
Uma aproximação de um número irracional pode ser obtida utilizando vários métodos de cálculo. No caso da série apresentada acima (para e), cada um dos infinitos termos do somatório é um valor positivo e diferente de zero. A soma destes infinitos termos nunca para de crescer, mas não ultrapassa um certo valor! O número e corresponde justamente a este valor que podemos calcular com grande precisão (para a série apresentada!) mas que somente nossa capacidade de abstração o captura por completo.
Ao longo do tempo várias pessoas investigaram como calcular o valor de certas séries:
--A série 1/1+1/1+1/2+1/6+1/24+1/120+... corresponde a base dos logaritmos naturais. Além da série 1+1/1!+1/2!+1/3!+... corresponde ao número e a série 1/1!+2/2!+3/3!+4/4!+5/5!+... e também a série 1+3/2!+5/4!+7/6!+9/8!+... Além disso o inverso da base dos logaritmos neperianos pode ser obtido com a série 1-1/1!+1/2!-1/3!+1/4!-1/5!+...
--A série 1/1+1/2+1/3+1/4+1/5+... não define nenhum valor e tende para o infinito (e além... está é a série harmônica).
--A série 1/2+1/4+1/8+1/16+1/32+... corresponde à unidade (a soma dos infinitos inversos das potências de 2 corresponde a 1).
Somente em 1735, foi encontrado o número que corresponde à série 1/1+1/4+1/9+1/16+1/25+... O somatório do inverso dos quadrados de todos os naturais corresponde a um sexto do quadrado de Pi. A soma de todos os inversos dos números naturais não é limitada (nem a soma de todos os inversos dos números naturais primos!), mas quando substituimos um número natural n por b^n (b elevado a n) ou quando substituimos os naturais por seus fatoriais, a soma de todos eles é limitada (para certos valores de b).
O programa acima utiliza a função fabs, aqui estão algumas outras funções disponíveis na biblioteca de funções da linguagem C:
sin(x) sine of x
cos(x) cosine of x
tan(x) tangent of x
asin(x) sin inverse (x) in range [-pi/2,pi/2], x in
[-1,1].
acos(x) cos inverse (x) in range [0,pi], x in
[-1,1].
atan(x) tan inverse (x) in range [-pi/2,pi/2].
atan2(y,x) tan inverse (y/x) in range [-pi,pi].
sinh(x) hyperbolic sine of x
cosh(x) hyperbolic cosine of x
tanh(x) hyperbolic tangent of x
exp(x) exponential function e^x
log(x) natural logarithm ln(x), x>0.
log10(x)
base 10 logarithm, x>0.
pow(x,y) x^y. A
domain error occurs if x=0 and y<=0, or if x<0 and y is not an integer.
sqrt(x) square root of x, x>=0.
ceil(x) smallest integer not less than x,
as a double.
floor(x) largest integer not greater than
x, as a double.
fabs(x) absolute value of x
ldexp(x,n) x*2^n
frexp(x, int *ip) splits x into a normalized fraction in the interval
[1/2,1) which is returned, and a power of 2, which is stored in *exp. If x is
zero, both parts of the result are zero.
modf(x, double *ip) splits x into integral and fractional parts, each with the same sign as x. It stores the integral part in *ip, and returns the fractional part. Exemplo:
double d=123.456; double inteira, frac;
frac=modf(d,
&inteira);
printf(“numero:%e parte inteira:%e parte
fracionaria:%e\n”, d, inteira, frac);
fmod(x,y) floating-point remainder of x/y, with the
same sign as x. If y is zero, the result is implementation-defined.
---
Na linguagem C, em alguns locais podem aparecer os comandos denominados comandos de salto (ou ainda comandos de desvio) / “jump statements”. Exemplos de “salto”: break , continue e return. O comando continue só pode aparecer dentro de um comando de iteração (pode aparecer no for, while ou do, não pode aparecer no switch). Quando o fluxo de controle atinge um comando continue o fluxo de controle irá desviar, no caso de while e do, para a parte de teste. Quando o continue está no escopo de um for sua execução corresponde a desviar para a parte de incremento (ou avaliação do terceiro elemento do for). O comando break pode aparecer dentro de um switch ou um comando iterativo. Quando o fluxo de controle atinge um comando break o fluxo de controle irá desviar para o comando que segue o final do bloco (termina a iteração). O salto executado pelo return será discutido no contexto de “registro de ativação” de funções mais à frente na disciplina.
---
Exercícios
Escreva um programa em C que lê um valor inteiro N e desenha um quadrado feito com asteriscos de tamanho NxN
exemplo
para N=2
**
**
Escreva 6 programas em C, cada programa lê um valor inteiro N e desenha um triângulo feito com asteriscos de altura N.
Exemplo de impressão para N=3:
* *
* *** *****
***
** *** **
** *** **
*** ***** ***
* * *
Aqui está um dos 6 programas:
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[]){
int N;
int
linha, col, aux;
printf("Altura
do triangulo:");
scanf("%d",&N);
aux
= N;
for(linha=1 ;
linha<=N ; linha++ ){
for(col=1; col<aux;
col++ ) printf(" ");
aux--;
for(col=1;
col<=2*linha-1; col++ ) printf("*");
printf("\n");
}
system("PAUSE");
return
0;
}
Escreva 6 programas em C, cada programa lê um valor inteiro N e desenha dois triângulos feitos com asteriscos de altura 2*N,
Exemplo de impressão para N=3:
* *
* *** *****
***
** *** **
** *** **
*** ***** ***
* * *
*** ***** ***
* * *
** *** **
** *** **
* *
* *** *****
***
Escreva um programa em C que lê um valor inteiro N e desenha um losango de altura N.
Uma boa fonte de exercícios para treino de programação usando estruturas de controle são os programas que geram sequências. Um dos tipos de sequências é a sequência de inteiros. O sítio da Web http:\\oeis.org coleciona um grande número de sequências e pode ser usado para verificar se o programa está gerando a sequência de forma correta. Por exemplo: escreva um programa em C que gera N termos da sequência de inteiros que considere inicialmente o valor 2 e os termos seguintes correspondem a soma 1, multiplique por 1, soma 2, multiplique por 2, e assim sucessivamente... Os termos iniciais desta sequência são 2, 3, 3, 5, 10, 13, 39 e 43. Esta sequência corresponde à página http://oeis.org/A019460.
Escreva um programa em C que imprima a soma dos primeiros termos da série 1/2!+2/3!+3/4!+4/5!+5/6!+... esta série uma vez completadas as infinitas somas J resulta na unidade!
Escreva um programa que calcula o fatorial de um número lido
do teclado:
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[]){
printf("Programa
para calculo de fatorial de um numero \n");
printf("Entre
com n:");
int n;
scanf("%d",
&n);
int fatn;
//calculo
printf("O
fatorial de %d e' %d\n", n, fatn);
system("PAUSE");
return 0;
}
Faça um programa que calcula o termo de ordem n da série de Fibonacci, com n lido do teclado. O termo de ordem zero é zero, o termo de ordem 1 é 1, o termo seguinte a dois termos dados corresponde à soma destes dois termos. Assim o termo de ordem 2 é 0+1, o termo de ordem 3 é 1+1, o termo de ordem 4 é 1+2, o termo de ordem 5 é 2+3, otermo de ordem 6 é 3+5 e assim sucessivamente.
O programa discutido para cálculo de e utiliza o comando do-while. Reescreva o programa usando o comando for.
O número Pi pode ser calculado através da série Pi=4*(1-1/3+1/5-1/7+1/9-1/11+…). Faça um programa que calcula quantos termos desta série são necessários para calcular Pi com 2, 3 e 4 casas decimais i.e. 3.14, 3.141 e 3.1415 Dica: são necessários mais de 600 termos para obter 3.14
Algumas formulas não devem ser
usadas em cálculo numérico por computador... sabe-se,
por exemplo, que as formulas abaixo são praticamente “inúteis” para cálculos
(em particular para grandes valores de x):
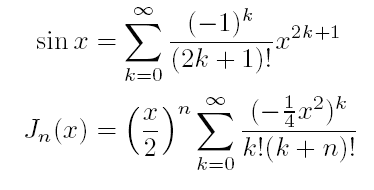
O número Pi pode ser calculado através da série Pi*Pi*Pi*Pi/90=1/1*1*1*1+1/2*2*2*2+1/3*3*3*3+1/4*4*4*4+1/5*5*5*5+… Faça um programa que calcula quantos termos desta série são necessários para calcular Pi com 2, 3, e 4 casas decimais.
Em 1995 Bailey, Borwein e Plouffe (BBP) derivaram uma nova fórmula para o cálculo de Pi:
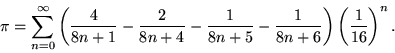
Faça um programa que mostre a rapidez da determinação dos dígitos de Pi para a fórmula de BBP em comparação com a fórmula de Euler determinada em 1735. Liste o valor aproximado de Pi para cada número de iterações. Com cerca de 11 iterações (depende da codificação!) a fórmula BBP esgota a capacidade do tipo double!
Vale a pena observar que a presença do último termo {(1/16)^n } faz com que seja possível o cálculo de digitos isolados de pi na base 16! (Não se conhece formula similar para a base 10). Procure na internet o artigo “Pi: A 2000-Year Search Changes Direction”, para ampliar a discussão.
Euler antes de descobrir o resultado de 1/1+1/4+1/9+1/16+1/25+... descobriu que precisava de muitos termos para conseguir determinar uns poucos dígitos. Quatro anos antes, em 1731, Euler conseguiu descobrir a equivalência da soma dos inversos dos quadrados dos naturais com a seguinte formula: ln(2)*ln(2) mais o somatório do inverso do produto do quadrado de k e dois elevado a k-1 (de k=1 até infinito). Esta fórmula de 1731 com poucos termos fornece vários dígitos de um sexto do quadrado de pi. Faça um programa que compara quantos termos devem ser somados para obter um sexto do quadrado de pi usando estas duas formulas.
---------------------
Faça um programa que comprove ser muito lenta a forma como o somatório dos termos da série harmônica vai para infinito. [1/1+1/2+1/3+1/4+1/5+1/6+1/7+1/8+1/9+…]
Isto pode ser feito de várias formas, p.ex. mostre o valor do somatório após a soma de mil, dez mil, cem mil, um milhão, dez milhões […] de termos. O somatório da seqüência dos inversos dos números primos não tem um limite, este somatório vai para o infinito muito, mas muito lentamente.
Se você pudesse fazer as operações de maneira razoavelmente precisa você poderia derivar a seqüência a seguir. Nesta seqüência para cada valor inteiro (1, 2, 3, ...) é mostrado quantos termos da série harmônica têm que ser somados para igualar ou ultrapassar este valor (não tenho certeza da precisão destes resultados!):
1:1, 2:4, 3:11, 4:31, 5:83, 6:227, 7:616, 8:1674, 9:4550, 10:12367, 11:33617, 12:91380, 13:248397, 14:675214, 15:1835421, 16:4989191, 17:13562027, 18:36865412, 19:100210581, 20:272400600, 21:740461601, 22:2012783315 ...
A lista abaixo mostra o tempo que leva em um computador pessoal comum para se conseguir acumular alguns valores. A primeira coluna é o somatório e a segunda coluna é a hora.
10 08:17:07
11 08:17:07
12 08:17:07
13 08:17:07
14 08:17:07
15 08:17:07
16 08:17:07
17 08:17:07
18 08:17:08
19 08:17:09
20 08:17:13
21 08:17:25
22 08:17:55
23 08:19:19
24 08:23:05
25 08:33:22
26 09:01:22
27 10:18:24
28 13:45:38
Observe que é da ordem de milisegundos
para passar do valor 13 para 14, de 14 para 15, de 15 para 16, de 16 para 17...
...mas leva-se mais de 1 hora para passar de 26 para
27 e leva-se mais de 3 horas para passar de 27 para 28!!! A lista abaixo mostra
a ordem de numero de termos necessários para adicionar uma unidade para o
somatório da série harmônica:
10 08:58:04 4742
11 08:58:04 12889
12 08:58:04 35035
13 08:58:04 95236
14 08:58:04 258877
15 08:58:04 703701
16 08:58:05 1912858
17 08:58:05 5199688
18 08:58:05 14134218
19 08:58:07 38420787
20 08:58:11 104438526
21 08:58:22 283893347
22 08:58:53 771702129
23 09:00:16 2097703872
24 09:04:03 5702150317
25 09:14:19 15500051598
26 09:42:13 42133508713
27 10:58:21 114530745186
28 14:29:31 311326745342
São necessários mais de 311 bilhões de termos para o somatório passar de 27 para 28, em um computador pessoal comum soma-los demora mais de 3 horas.
Colocado de outra forma: seja H(n) a soma dos n primeiros termos da série harmônica. H(1)=1, H(2)=1.5, H(3)=1.83333..., H(4)=2.0833...,
Para H(n)>20 uma boa aproximação é H(n)=ln(n)+gamma [gamma=0.5772....]
assim H(1 bilhão)~21, H(1 trilhão)~28, H(1 quatrilhão)~35, H(1quintilhão)~42, ...
A série harmônica tem relação com o logaritmo natural. A misteriosa constante gama é definida da seguinte forma:
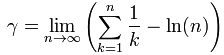
Não é necessário grande esforço para ver que esta constante corresponde a área da região em azul na figura abaixo (figuras da Wikipédia):
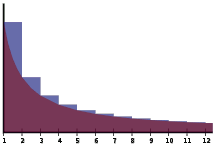
O logaritmo de n vai para o infinito quando n vai para infinito, o somatório dos primeiros n termos da série harmônica vai para infinito quando n vai para infinito, mas a diferença entre estes dois objetos quando n vai para infinito define a constante gama. Você poderá ficar famoso se descobrir certos fatos sobre esta contante... Ninguém sabe se esta constante é racional ou irracional!!! O valor de gama (wikipedia) é 0.57721566490153286060651209008240243104215933593992… (sequence A001620 no OEIS). Faça um programa para verificar se a diferença entre o somatório dos n primeiros termos da série harmônica e o logaritmo natural de n convergem de maneira rápida ou lenta para o valor fornecido de gama.
Faça um programa que mostra até onde podemos calcular, usando o tipo long long int um fatorial (até 20??? ):
fatorial(20)=2432902008176640000
(ou seja 2.4 quintilhões!)
O fatorial de 20 tem 19 dígitos. Se voce tentar calcular o fatorial de 21 o conteúdo da variável do tipo long “estoura” ???.
Faça um programa que mostre que podemos calcular, sem muita precisão de dígitos, usando o tipo double, o fatorial até 170:
fatorial(170)=7.257415615307994E306
Observe que o fatorial de 170 possui 307 dígitos, usando o tipo double temos somente cerca de 16 dos dígitos mais significativos. Abaixo apresentamos o fatorial de 170:
7257415615307998967396728211129263114716991681296451376543577798900561843401706157852350749242617459511490991237838520776666022565442753025328900773207510902400430280058295603966612599658257104398558294257568966313439612262571094946806711205568880457193340212661452800000000000000000000000000000000000000000
Devemos ter muito cuidado nas iterações, pois os erros podem se acumular e invalidar resultados aparentemente simples. Observe o programa abaixo e o resultado. Explique como que o erro inicialmente da ordem de 1E-16 cresce cerca de uma ordem de grandeza a cada iteração.
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[]){
double erroAcum;
double umSexto=1./6.;
int i;
for(i=1; i<21; i++){
umSexto=7.*umSexto-1.;
erroAcum=umSexto-1./6.;
printf("%e
%e\n", umSexto, erroAcum);
}
system("PAUSE");
return 0;
}
1.666667e-001
-5.551115e-017
1.666667e-001 -4.440892e-016
1.666667e-001 -3.164136e-015
1.666667e-001 -2.220446e-014
1.666667e-001 -1.554867e-013
1.666667e-001 -1.088463e-012
1.666667e-001 -7.619294e-012
1.666667e-001 -5.333511e-011
1.666667e-001 -3.733459e-010
1.666667e-001 -2.613421e-009
1.666666e-001 -1.829395e-008
1.666665e-001 -1.280576e-007
1.666658e-001 -8.964034e-007
1.666604e-001 -6.274824e-006
1.666227e-001 -4.392377e-005
1.663592e-001 -3.074664e-004
1.645144e-001 -2.152265e-003
1.516008e-001 -1.506585e-002
6.120570e-002 -1.054610e-001
-5.715601e-001 -7.382268e-001
Press any key to continue . . .
-----
Voltando às séries infinitas, é interessante observar
1-1/2+1/3-1/4+1/5-1/6+...= ln(2)
1-1/3+1/5-1/7+1/9-1/11+...=pi/4
Durante anos procurou-se descobrir o resultado da soma dos inversos dos quadrados da sequência dos naturais:
1/1*1+1/2*2+1/3*3+1/4*4+1/5*5+...
somente em 1734 foi que Euler, aos 27 anos, mostrou que o resultado era um sexto do quadrado de pi (pi*pi/6).
A partir do resultado de Euler foi menos extenuante descobrir que
1/1*1+1/3*3+1/5*5+1/7*7+1/9*9+...=pi*pi/8
1/2*2+1/4*4+1/6*6+1/8*8+1/10*10+...=pi*pi/24
1/1*1-1/2*2+1/3*3-1/4*4+1/5*5-1/6*6+...=pi*pi/12
Faça alguns programas que mostram a velocidade de convergência das expressões acima
---
Faça alguns exercícios relacionados a uma implementação “precária” do jogo-da-velha.