- (a)
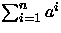
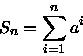
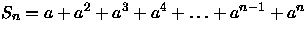
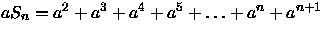
aSn-Sn=an+1-a
Sn(a-1)=a(an-1)
para a > 1,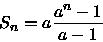
Sn=n
para a = 1.
- (b)
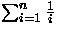
A resolução deste somatório pode ser efetuada utilizando a aproximação por integral [CLR90], onde temos que: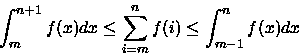
assim,
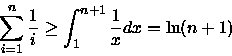
(1) e
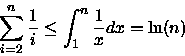
(2) 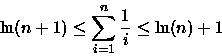
ou seja,
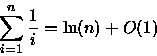
- (c)
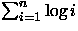
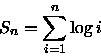
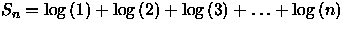
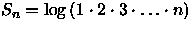
Pela aproximação de Stirling [CLR90] pode-se escrever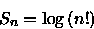
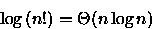
- (d)
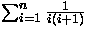
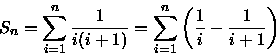
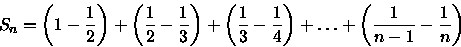
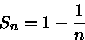
- (a)
-
PROCEDURE FazAlgo ( n : integer); VAR i, j, k, x : integer; BEGIN x := 0; FOR i := 1 TO n - 1 DO FOR j := i + 1 TO n DO FOR k := 1 TO j DO x := x + 1; END;Analisando o número de vezes que a variável x é incrementada, a um custo O(1), tem-se
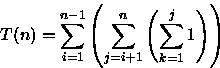
Fazendo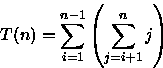
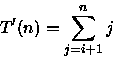
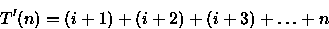
![\begin{displaymath}
T'(n)=(n-i)\left[\frac{(i+1)+n}{2}\right]\end{displaymath}](img26.gif)
então,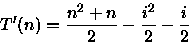
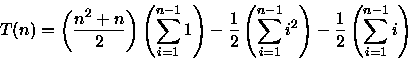
fazendo
![$\sum_{i=1}^{n-1}i^2 = \frac{(n-1)(n)[2(n-1)+1]}{6}$](img29.gif) [Knu73], tem-se
[Knu73], tem-se
![\begin{displaymath}
T(n)=\left(\frac{(n^{2}+n)}{2}(n-1)\right) - \frac{1}{2}\lef...
...+1]}{6}\right) - \frac{1}{2}\left(\frac{(n-1)(1+n-1)}{2}\right)\end{displaymath}](img30.gif)
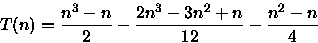
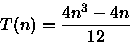
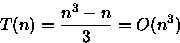
- (b)
-
PROCEDURE Pesquisa ( n : integer); BEGIN IF n > 1 THEN BEGIN Inspecione n*n*n elementos; // custo n^3 Pesquisa (n/3); END; END;Neste algoritmo é necessário analisar o número de inspeções feitas. Assim, considerando que a inspeção de um único elemento tem custo O(1), a seguinte relação de recorrência pode ser montada:
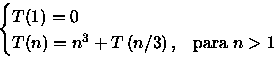

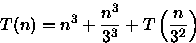
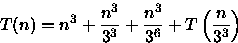
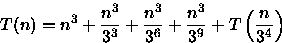
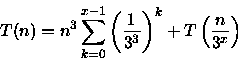
Como T(1)=0, fazendo n=3x tem-se
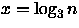 então
então
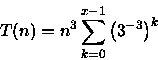
![\begin{displaymath}
T(n)=n^{3}\left[\frac{\left(3^{-3}\right)^{x}-1}{3^{-3}-1}\right]\end{displaymath}](img42.gif)
![\begin{displaymath}
T(n)=\frac{27n^{3}}{26}\left[1 - \left(3^{-3}\right)^{x}\right]\end{displaymath}](img43.gif)
![\begin{displaymath}
T(n)=\frac{27n^{3}}{26}\left[1 - \left(3^{x}\right)^{-3}\right]\end{displaymath}](img44.gif)
![\begin{displaymath}
T(n)=\frac{27n^{3}}{26}\left[1 - n^{-3}\right]\end{displaymath}](img45.gif)
![\begin{displaymath}
T(n)=\frac{27}{26}\left[n^{3} - 1\right]=O(n^{3})\end{displaymath}](img46.gif)
- (c)
-
PROCEDURE Sort ( VAR A: ARRAY[1..n] OF integer; i, j: integer ); { n uma potencia de 2 } BEGIN IF i < j THEN BEGIN m := (i + j - 1)/2; Sort(A,i,m); // custo = T(n/2) Sort(A,m+1,j); // custo = T(n/2) Merge(A,i,m,j); // custo = n-1 comparacoes no // pior caso { Merge intercala A[i..m] e A[m+1..j] em A[i..j] } END; END;Para este algoritmo é importante observar o número de comparações feitas para ordenar o vetor. Observe que este algoritmo divide o vetor em duas partes, ordena e combina estas partes através do procedimento Merge que faz no pior caso n-1 comparações. Assim, a relação de recorrência para este algoritmo é:
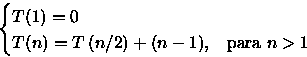
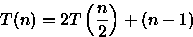
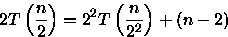
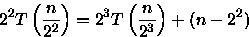

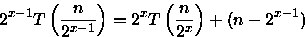
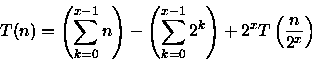
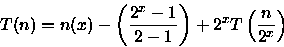
Considerando que n é uma potência de 2, ou seja, n=2x, tem-se que
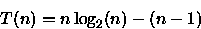
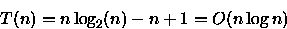
- (d)
-
PROCEDURE Proc( n : integer ); BEGIN IF n = 0 THEN RETURN 1 ELSE RETURN Proc(n-1) + Proc(n-1) END;Neste algoritmo a medida de tempo pode ser considerada como o número de vezes em que é feita a soma da recursão Proc(n-1) + Proc(n-1). Portanto, a relação de recorrência para este algoritmo é:
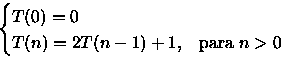
T(n)=2T(n-1) + 20
2T(n-1)=22T(n-2) + 21
22T(n-2)=23T(n-3) + 22
23T(n-3)=24T(n-4) + 23
24T(n-4)=25T(n-5) + 24

2n-1T(1)=2nT(0) + 2n-1
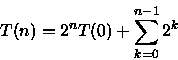
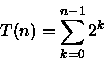
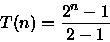
T(n)=2n - 1 = O(2n)
São dados 2n números distintos distribuídos em dois arranjos A e B, cada um com n elementos ordenados, tal que:
- (a)
- Apresente um algoritmo ótimo para resolver esse problema. Implemente o seu algoritmo.
A listagem da implementação deve ser entregue e o programa submetido.
Algoritmo
Elemento nEsimoMaiorElementoR(Arranjo A, Arranjo B, Indice inicioA, Indice fimA, Indice inicioB, Indice fimB) { (1) int tamanhoAB, pivoA, pivoB; (2) tamanhoAB = fimA - inicioA + 1; (3) pivoA =(tamanhoAB != 1)?(tamanhoAB/2 + inicioA - 1):inicioA; (4) pivoB =(tamanhoAB != 1)?(tamanhoAB/2 + inicioB - 1):inicioB; /* A condicao de parada e quando restam dois ou menos elementos a serem comparados */ (5) if( tamanhoAB == 1 ) { (6) return (A[pivoA] > B[pivoB]) ? A[pivoA] : B[pivoB]; (7) } (8) if( A[pivoA] > B[pivoB] ) { /* Elimina os ganhadores de A e os perderores de B */ (9) fimB -= pivoA - inicioA + 1; (10) inicioA = pivoA + 1; (11) } else { /* Elimina os ganhadores de B e os perderores de A */ (12) fimA -= pivoB - inicioB + 1; (13) inicioB = pivoB + 1; (14) } /* Aplica novamente o algoritmo na metade restante do problema */ (15) return nEsimoMaiorElementoR(A,B,inicioA,fimA,inicioB,fimB); }
Análise de complexidade
Para a análise do custo será considerado o número de comparações entre os elementos de A e de B. Assim, pela linha (6) temos que T(1) = 1. Na linha (8) é feita uma única comparação e, nas linhas (9) e (10) metade dos elementos de A e B são descartados. A seguir, na linha (15) o algoritmo é aplicado novamente nas metades restantes de A e B de maneira que T(n) = 1 + T(n/2) para n>1. Desta forma a relação de recorrência para o algoritmo é
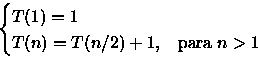
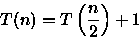
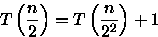
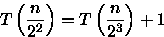

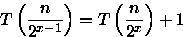
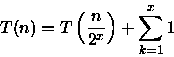
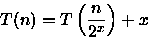
Assumindo que n é uma potência de 2, ou seja, n = 2x (resultando em
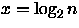 ), temos que
), temos que
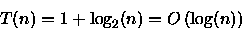
(3)
Descrição geral e decisões de projeto
Para facilitar a legibilidade e a análise da complexidade, o algoritmo foi escrito de forma recursiva. O ambiente de desenvolvimento e de testes utilizado foi uma estação UltraSparc da SUN com sistema operacional Unix. A linguagem de implementação foi o C utilizando o compilador gcc.
Com o objetivo de simplificar a implementação respeitando de forma fiel à especificação do problema (especificação da questão 3) os arranjos foram gerados com N+1 elementos sendo considerado apenas os elementos de índice 1 a N.
Descrição dos módulos
O programa implementado é constituído de dois módulos:
- i.
- rand - formado pelos arquivos rand.c (fornecido pelo professor) e rand.h. O arquivo rand.c possui a implementação das funções de geração de valores aleatórios enquanto o arquivo rand.h possui o cabeçalho destas funções.
- ii.
- nmaior - formado pelos arquivos nmaior.c e nmaior.h. O arquivo nmaior.c apresenta a implementação das funções relacionadas com o problema de encontrar o n-ésimo maior elemento. O arquivo nmaior.h disponibiliza o cabeçalhos das funções definidas em nmaior.c e a definição dos tipos de dados.
- iii.
- main - inclui o arquivo main.c com o programa principal.
O módulo rand é utilizado somente pelo módulo nmaior. O módulo principal (main) faz uso direto apenas do módulo nmaior.
Tipos de dados utilizados
No arquivo nmaior.h são definidos os seguintes tipos de dados e constantes:
- N - constante que define o tamanho dos elementos.
- Elemento - inteiro do tipo int. Define um elemento do Arranjo.
- Indice - inteiro do tipo int. Define o tipo usado para indexar os elementos dos Arranjos.
- Arranjo - vetor do tipo Elemento. Define um arranjo com N+1 elementos dos quais serão considerados
apenas os elementos de índices i com
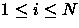 .
.
Descrição do formato de entrada
Os arranjos A e B são gerados automaticamente basta definir o valor da constante N no arquivo nmaior.h.
Descrição do formato de saída
A saída é textual seguindo o formato abaixo.
Arranjo A: 4065 2031 1011 499 245 113 51 21 5 1 Arranjo B: 6318 3158 1570 782 388 190 94 42 12 0 O 10o. maior elemento em O(lg(N)) eh: 245
Utilização do programa
Após compilado, basta executar a seguinte linha de comando: ``./main''.
Listagem de Testes
A seguir são listados alguns testes executados.
Arranjo A: 4065 2031 1011 499 245 113 51 21 5 1 Arranjo B: 6318 3158 1570 782 388 190 94 42 12 0 O 10o. maior elemento em O(lg(N)) eh: 245
Arranjo A: 100 95 90 85 80 Arranjo B: 10 9 8 7 5 O 5o. maior elemento em O(lg(N)) eh: 80
Arranjo A: 100 95 89 85 Arranjo B: 101 90 81 75 O 4o. maior elemento em O(lg(N)) eh: 90
Arranjo A: 87 8 7 5 1 Arranjo B: 777 654 92 89 75 O 5o. maior elemento em O(lg(N)) eh: 87
- (b)
- Prove que o seu algoritmo é ótimo, isto é, obtenha um limite inferior para o número de comparações para resolver esta classe de problemas.
Figura: Possíveis soluções para o problema da questão 3. Os elementos maiores do que o n-ésimo são, para este problema, irrelevantes (representados aqui pelo símbolo ``?''). Portanto, existem apenas 2n possíveis soluções. ![\begin{figure}
\begin{displaymath}
\begin{array}
{cc}
S_{1} = <?;~?;~?;~\ldot...
... S_{n+n} = <?;~?;~?;~\ldots; B[n]\gt
\end{array} \end{displaymath} \end{figure}](img73.gif)
Para encontrar o limite inferior para este problema podemos utilizar a árvore de decisão [CLR90].
Montagem da árvore de decisão
A árvore de decisão representa o número de comparações entre elementos de A e de B quando o algoritmo opera sobre uma entrada de tamanho n. Na árvore de decisão, cada nodo é denotado por (A[i]:B[j]) para algum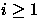 e
e 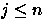 . Cada nó-folha da árvore representa uma das possíveis soluções (figura 1) com os n
maiores elementos de A e B e são denotados por
. Cada nó-folha da árvore representa uma das possíveis soluções (figura 1) com os n
maiores elementos de A e B e são denotados por ![$<?;~?;~?;~\ldots; A[k]\gt$](img76.gif) ou
ou
![$<?;~?;~?;~\ldots; B[k]\gt$](img77.gif) onde
onde 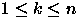 , A[k] ou B[k] é o n-ésimo maior elemento e ``?''
representam os elementos maiores do que ele. Assim, o total de nós-folhas é 2n. Como todos os elementos de
A e B são distintos, nos interessa somente a comparação A[i]<B[j] ou A[i]>B[j]. A execução do algoritmo
ótimo corresponde a um caminho qualquer
do nó-raiz a um nó-folha. Em cada nodo a comparação A[i]<B[j] é feita. A sub-árvore da esquerda indica as
possíveis comparações subseqüentes para A[i]<B[j]. A sub-árvore da direita indica as possíveis comparações
subseqüentes para A[i]>B[j]. Note que montando a árvore de decisão
desta maneira, ela é mínima, ou seja, não existe duas computações que possam levar a respostas equivalentes.
Ou de maneira mais formal:
, A[k] ou B[k] é o n-ésimo maior elemento e ``?''
representam os elementos maiores do que ele. Assim, o total de nós-folhas é 2n. Como todos os elementos de
A e B são distintos, nos interessa somente a comparação A[i]<B[j] ou A[i]>B[j]. A execução do algoritmo
ótimo corresponde a um caminho qualquer
do nó-raiz a um nó-folha. Em cada nodo a comparação A[i]<B[j] é feita. A sub-árvore da esquerda indica as
possíveis comparações subseqüentes para A[i]<B[j]. A sub-árvore da direita indica as possíveis comparações
subseqüentes para A[i]>B[j]. Note que montando a árvore de decisão
desta maneira, ela é mínima, ou seja, não existe duas computações que possam levar a respostas equivalentes.
Ou de maneira mais formal:
Sejam Alg o algoritmo usado para montar a árvore de decisão acima, Si = Alg(A,B) a solução do algoritmo, Ci o caminho percorrido para encontrar Si e n o tamanho de A e B. A árvore montada acima possui as seguintes características:- i.
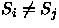 para todo
para todo 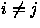 com
com 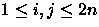 .
.
- ii.
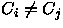 para todo
para todo 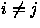 com
com 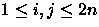 .
.
- iii.
- Pelos ítens (i) e (ii), se Si = Alg(A,B) e Sj = Alg(A,B), então i = j para todo
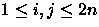 .
. - iv.
- Os ítens (i) e (ii) implicam que a árvore de decisão é mínima e Alg é ótimo.
Limite inferior para o pior caso
O comprimento do maior caminho do nó-raiz da árvore de decisão para seus nós-folhas representa o pior caso de número de comparações entre elementos de A e de B. Por conseqüência, o pior caso do algoritmo ótimo corresponde a altura h da sua árvore de decisão. A árvore de decisão montada, é uma árvore binária e, portanto, não possui mais de 2h nós folhas. Como o número de nós-folhas da árvore é 2n podemos escrever
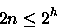
(4) ou seja,
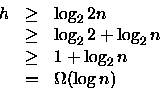
(5) Conforme o custo obtido em (3) o algoritmo apresentado no item (a) da questão 3 é ótimo.
Considere o algoritmo para pesquisar e inserir registros em uma árvore binária de pesquisa sem balanceamento. Devido à sua simplicidade e eficiência a árvore binária de pesquisa é considerada uma estrutura de dados muito útil. Considerando-se que a altura da árvore corresponde ao tamanho da pilha necessária para pesquisar na árvore é importante conhecer o seu valor. Assim sendo,
- (a)
- Determine empiricamente a altura esperada da árvore;
Metodologia utilizada
Para determinar a altura da árvore de forma empírica, foram utilizados valores de n (número de nós) tais que n = 2i com
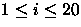 . Para cada
valor de n foram geradas 50 árvores randômicas calculando-se a altura média
he(n) (tabela 1). Admitindo que a altura esperada é
. Para cada
valor de n foram geradas 50 árvores randômicas calculando-se a altura média
he(n) (tabela 1). Admitindo que a altura esperada é
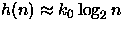 foi calculado o valor de k0 para cada n. Pelos
valores de k0 exibidos na tabela 1 e a curva da
figura 5, percebemos que k0 cresce com o valor n
contudo, quanto maior o valor de n menor é o crescimento de k0 sugerindo
que quando n tende a infinito, o valor de k0 é realmente constante. Assim,
o valor de k0 torna-se significativo quando n cresce, tendendo ao infinito.
Para os valores simulados podemos calcular um k0-medio da seguinte forma:
foi calculado o valor de k0 para cada n. Pelos
valores de k0 exibidos na tabela 1 e a curva da
figura 5, percebemos que k0 cresce com o valor n
contudo, quanto maior o valor de n menor é o crescimento de k0 sugerindo
que quando n tende a infinito, o valor de k0 é realmente constante. Assim,
o valor de k0 torna-se significativo quando n cresce, tendendo ao infinito.
Para os valores simulados podemos calcular um k0-medio da seguinte forma:
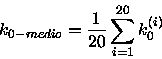
onde k0(i) são os valores da tabela 1.
Tabela: Altura média da arvore onde n é número de nós da árvore, he(n) é altura média empírica, hb(n) é altura da árvore binária balanceada e 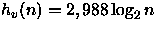 é a altura esperada
utilizando a constante encontrada na literatura.
é a altura esperada
utilizando a constante encontrada na literatura.n he(n) hb(n) hv(n) k0(n) 2 1 1 3 1,000 4 3 2 6 1,085 8 4 3 9 1,260 16 6 4 12 1,488 32 9 5 15 1,662 64 11 6 18 1,738 128 14 7 21 1,913 256 17 8 24 2,001 512 19 9 27 2,051 1024 21 10 30 2,095 2048 24 11 33 2,165 4096 27 12 36 2,193 8192 30 13 39 2,287 16392 33 14 42 2,294 32784 35 15 45 2,325 65536 38 16 48 2,364 131072 42 17 51 2,429 262144 44 18 54 2,428 524288 47 19 57 2,426 1048576 50 20 60 2,467
Figura: Gráfico da altura da árvore binária randômica sem balanceamento. A curva dos valores esperados foi desenhada utilizando a constante encontrada na literatura (k=2,988). ![\begin{figure}
\centering
\includegraphics [scale=0.75]{images/empxespxbal.eps}
\end{figure}](img89.gif)
- (b)
- Mostre analiticamente o melhor caso e o pior caso para a altura da
árvore;
Algoritmo de inserção
void Insere(Registro x, Apontador *p) { if (*p == NULL) { *p = (Apontador) malloc(sizeof(Nodo)); (*p)->Reg = x; (*p)->Esq = NULL; (*p)->Dir = NULL; return; } if (x.Chave < (*p)->Reg.Chave) { Insere(x, &(*p)->Esq); return; } if (x.Chave > (*p)->Reg.Chave) Insere(x, &(*p)->Dir); else printf(" Erro : Registro %d ja existe na arvore\n", x.Chave); } /* Insere */Pior caso
Analisando o algoritmo de inserção,o pior caso é quando os valores inseridos na árvore em ordem crescente ou decrescente resultando em uma lista linear, ou seja, h = n. Quando em ordem crescente, os elementos são inseridos sempre a esquerda da árvore. Quando em ordem decrescente, os elementos são inseridos sempre a direita da árvore. A figura 3 mostra um exemplo do pior caso da árvore binária randômica sem balanceamento.
Melhor caso
Novamente recorrendo ao algoritmo de inserção, o melhor caso é quando os elementos são inseridos de forma que a árvore resultante seja balanceada, neste caso, a relação da altura com o número de nós é mostrada na tabela 2 de onde podemos concluir que n = 2h+1-1, ou seja,
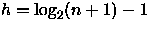 . A figura 4
mostra um exemplo do melhor caso quando a árvore fica balanceada.
. A figura 4
mostra um exemplo do melhor caso quando a árvore fica balanceada.
Tabela: Relação da altura da árvore binária balanceada com o número de nós. h (altura) n (número de nós) 1 1 3 2 7 3 15
- (c)
- Compare os resultados obtidos no item (a) com resultados analíticos publicados na
literatura.
Em [Dev86,Drm01,Drm02] é dito que quando n tende a infinito a altura esperada é
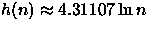 ou
ou 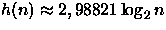 . Veja que os valores
simulados sugerem um crescimento da constante proporcional ao valor de n, contudo,
podemos observar que quanto maior o valor de n menor é o crescimento da constante
k0 de maneira que quando n tende a infinito, o valor de k0 torna-se
independente do valor de n. Assim, os valores obtidos em simulação são coerentes
com o valor encontrado na literatura (figura 5).
A figura 5 mostra o comportamento da constante (obtido em simulação)
em relação ao valor 4.31107.
. Veja que os valores
simulados sugerem um crescimento da constante proporcional ao valor de n, contudo,
podemos observar que quanto maior o valor de n menor é o crescimento da constante
k0 de maneira que quando n tende a infinito, o valor de k0 torna-se
independente do valor de n. Assim, os valores obtidos em simulação são coerentes
com o valor encontrado na literatura (figura 5).
A figura 5 mostra o comportamento da constante (obtido em simulação)
em relação ao valor 4.31107.
Figura: Comportamento da constante para os valores de n simulados, k0 foi obtido pela simulação e k é o valor obtido na literatura. ![\begin{figure}
\centering
\includegraphics [scale=0.8]{images/constante-altura.eps}\end{figure}](img95.gif)
- (d)
- Mostre analiticamente o número esperado de comparações para encontrar um registro
existente na árvore (busca com sucesso).
Definições
Para demonstrar o número esperado de comparações da busca com sucesso serão necessárias algumas definições enunciadas em [Knu73].
Nó Interno (Internal Node). Um nó que não é raiz nem folha da árvore binária.
Nó Externo (External Node). Um nó folha da árvore binária.
Comprimento de Caminho Externo (External Path Length) doravante referenciado por
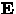 . Constitui a soma de todos os caminhos do nó-folha de uma árvore binária
para cada nó-externo.
. Constitui a soma de todos os caminhos do nó-folha de uma árvore binária
para cada nó-externo.
Comprimento de Caminho Interno (Internal Path Length) doravante referenciado por
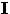 . Constitui a soma de todos os caminhos do nó-folha de uma árvore binária
para cada nó-interno.
. Constitui a soma de todos os caminhos do nó-folha de uma árvore binária
para cada nó-interno.
A relação entre o Comprimento de Caminho Externo e o Comprimento de Caminho Interno de uma árvore binária é
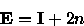
(6) onde n é o número de nós da árvore.
Considerando Cn o número médio de comparações em uma busca com sucesso e Cn' o número médio de comparações em uma busca sem sucesso.
Em uma busca por uma chave, assumindo que cada um dos n nós pode conter a chave procurada com a mesma probabilidade. Podemos definir:
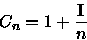
(7) 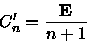
(8) 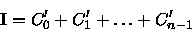
(9) Pelas e as equações (6), (7) e (8) obtemos
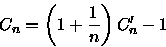
(10) Pelas equações (7) e (9) obtemos
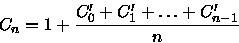
(11) 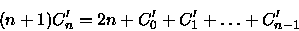
(12) Subtraindo (12) por
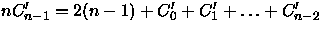 obtemos
obtemos
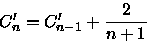
(13) Como C0'=0 podemos facilmente chegar em
Cn' = 2Hn - 2 (14) Substituindo (14) em (10) obtemos
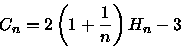
(15) onde Hn é o número harmônico. Pelo exercício 1, item (b),
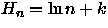 , então
, então
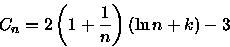
considerando n grande (tendendo a infinito), temos
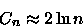
mudando o logaritmo para base 2
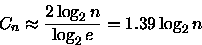
![\begin{figure}
\centering
\includegraphics [scale=0.8]{images/pior-caso-arvore.eps}\end{figure}](img90.gif)
![\begin{figure}
\centering
\includegraphics [scale=0.8]{images/melhor-caso-arvore.eps}\end{figure}](img92.gif)