Marcus Vinícius de Melo Rocha
mvrocha@dcc.ufmg.br
marcus@limiar.com.br http://www.limiar.com.br
20 de julho de 2002
INT r[N], i;
i= 1;
r[i]= escolhe(r,0);
SE falha() ENTAO ABORTAR;
PARA (i=2; i<=N; i++)
r[i]= escolhe(r,i);
SE falha() ENTAO ABORTAR;
FIM;
A rotina escolhe seleciona a próxima cidade do caminho. Ela recebe, como parâmetro, a lista de
cidades já selecionadas ((r,0) ou (r,i)). Sendo a complexidade de escolhe
Esta transformacão pode ser feita em tempo polinomial (
PARA "cada vertice v de G"
PARA "cada vertice u adjacente a v"
SE "nao existe aresta (u,v)"
ENTAO "Criar aresta (u,v) com peso 2"
SE "existe aresta (u,v) sem peso atribuido"
ENTAO "Atribuir peso 2 para a aresta"
|
DEPTH FIRST SEARCH - DFS. É
tradicionalmente empregada para busca exaustiva no espaço de solução de problemas DFS), quanto a busca em largura
(BREADTH FIRST SEARCH - BFS) são casos particulares dos algoritmos conhecidos como
BRANCH AND BOUND, e podem ser usadas neste tipo de pesquisa.
|
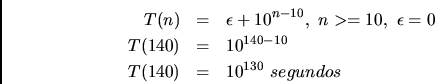

#define K_MAX_ADJ 500
typedef char T_NomeExp [256];
typedef char T_DescrExp [256];
typedef int T_MADJ [K_MAX_ADJ+1][K_MAX_ADJ+1];
int N; // Nro de vertices
T_MADJ MADJ; // Matriz de adjacências
int minC; // O menor custo ja encontrado para uma rota
int marca [K_MAX_ADJ+1]; // Para controlar o caminhamento do NN
int rota [K_MAX_ADJ+1]; // Para registrar a rota em otimizaçao
int agora; // Profundidade atual do NN
void NN(int v) {
int c, i, j, cf, melhor, onde;
c= 0; // Ainda sem custo
agora= 0; // O primeiro na rota
rota[++agora]= v;
marca[v]= 1; // Já foi visitado
onde= v;
for (i=1; i<N; i++) {
cf= MAXINT;
melhor= 0;
for (j=1; j<=N; j++) { // Varrer cada filho
if (j != onde) {
if (!marca[j]) { // Apenas os ainda não visitados
if (MADJ[onde][j] < cf) { // Escolher o mais economico
cf= MADJ[onde][j]; melhor= j;
}
}
}
}
onde= melhor; marca[onde]= 1; rota [++agora]= onde; c+= cf;
}
minC= c + MADJ[onde][v]; // Fechar o ciclo
}
|
for externo que varre cada um dos vértices, e um interno que varre cada um dos adjacentes ao vértice
selecionado na varredura externa. Como o grafo é completo, cada vértice tem for mais interno é 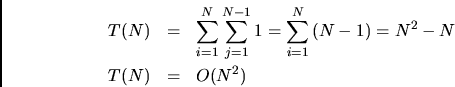
int BuscaLocal_3_opt() {
int melhora, algumaMelhora;
int maxo1, maxo2, maxo3;
int o1, d1, o2, d2, o3, d3;
algumaMelhora= 0; melhora= 1;
maxo1= N-5; maxo2= N-3; maxo3= N-1;
while (melhora) {
melhora= 0;
for (o1=1; o1<=maxo1; o1++) {
d1= o1+1;
for (o2=d1+1; o2<=maxo2; o2++) {
d2= o2+1;
for (o3=d2+1; o3<=maxo3; o3++) {
d3= o3+1;
if (Trocar3Arestas(o1,d1,o2,d2,o3,d3)) {
algumaMelhora= 1;
}
}
}
}
}
return (algumaMelhora);
}
|
Trocar3Arestas é Trocar3Arestas é
um ponto crítico no desempenho global da heurística mas, a menos que sua implementação seja totalmente
descuidada e patológica, não alterará a ordem de complexidade do algoritmo, e será constante, ou
ao menos aproximadamente constante, para quaisquer três arestas trocadas, independente de 
Passamos, agora, ao algoritmo
int BuscaLocal_4_opt() {
int melhora, algumaMelhora;
int maxo1, maxo2, maxo3, maxo4;
int o1, d1, o2, d2, o3, d3, o4, d4;
int trocaFeita;
maxo1= N-7; maxo2= N-5; maxo3= N-3; maxo4= N-1;
algumaMelhora= 0; melhora= 1;
while (melhora) {
melhora= 0;
for (o1=1; o1<=maxo1; o1++) {
d1 = o1+1;
for (o2=d1+1; o2<=maxo2; o2++) {
d2 = o2+1;
for (o3=d2+1; o3<=maxo3; o3++) {
d3 = o3+1;
for (o4=d3+1; o4<=maxo4; o4++) {
d4 = o4+1;
if (Trocar4Arestas(o1,d1,o2,d2,o3,d3,o4,d4)) {
algumaMelhora= 1;
}
}
}
}
}
}
return(algumaMelhora);
}
|
Trocar4Arestas(o1,d1,o2,d2,o3,d3,o4,d4)
tem custo constante para quaisquer que sejam as arestas
trocadas2, e que for externos de for interno
que varre a matriz de adjacências, em busca da quarta aresta a trocar. Ou, vendo de outra forma, temos o for externo, que repete os três for internos, de complexidade
int j, melhora, melhora3, melhora4, vez3, vez4;
int savRota [K_MAX_ADJ+1]; // Para registrar a rota em otimização
int savC, i;
//Inicializacao de NN
for (j=1; j<=N; j++) marca[j]= 0;
minC= MAXINT;
//Gera a solucao NN originada em cada vertice do grafo, e
// fica com a melhor para dar partid na otimizacao
NN(1);
for (i=2; i<=N; i++) {
savC= minC;
for (j=1; j<=N; j++) marca[j]= 0;
minC= MAXINT;
NN(i);
if ("MELHOR QUE ANTERIOR") {
"SUBSTITUI ANTERIOR PELA ATUAL";
}
}
//Otimiza com 3_opt e 4_opt enquanto for possivel
melhora= 1;
while (melhora) {
melhora= BuscaLocal_3_opt();
if (!melhora) {
melhora= BuscaLocal_4_opt();
if (melhora) {
melhora= BuscaLocal_3_opt();
}
}
}
return (minC);
}
| 424 | 176 | 136 | 353 | 199 | 35 | 212 | 49 | 48 | 144 | 143 | 98 | 89 | 404 | 366 | ||
| 302 | 243 | 263 | 170 | 214 | 82 | 94 | 97 | 309 | 120 | 145 | 210 | 117 | 296 | 430 | ||
| 36 | 399 | 365 | 148 | 295 | 335 | 244 | 234 | 9 | 84 | 27 | 10 | 150 | 149 | 12 | ||
| 371 | 361 | 41 | 328 | 311 | 246 | 185 | 147 | 192 | 180 | 127 | 200 | 81 | 305 | 162 | ||
| 139 | 307 | 163 | 95 | 403 | 205 | 409 | 187 | 238 | 93 | 19 | 287 | 189 | 441 | 394 | ||
| 392 | 388 | 186 | 52 | 116 | 344 | 245 | 233 | 174 | 46 | 157 | 131 | 225 | 118 | 401 | ||
| 74 | 159 | 106 | 324 | 160 | 406 | 407 | 390 | 382 | 161 | 85 | 56 | 175 | 268 | 223 | ||
| 347 | 319 | 317 | 134 | 58 | 201 | 50 | 313 | 38 | 44 | 92 | 340 | 393 | 389 | 215 | ||
| 101 | 22 | 91 | 6 | 299 | 251 | 273 | 68 | 99 | 364 | 206 | 59 | 121 | 16 | 286 | ||
| 220 | 345 | 114 | 277 | 102 | 376 | 440 | 195 | 100 | 301 | 25 | 326 | 239 | 54 | 28 | ||
| 190 | 87 | 126 | 53 | 76 | 153 | 13 | 42 | 209 | 230 | 292 | 242 | 40 | 14 | 3 | ||
| 322 | 124 | 198 | 140 | 370 | 318 | 179 | 135 | 351 | 253 | 323 | 216 | 204 | 80 | 285 | ||
| 248 | 298 | 235 | 164 | 280 | 358 | 259 | 47 | 67 | 45 | 291 | 261 | 304 | 154 | 29 | ||
| 5 | 2 | 1 | 11 | 155 | 282 | 270 | 327 | 294 | 348 | 249 | 17 | 60 | 436 | 349 | ||
| 360 | 300 | 308 | 226 | 346 | 247 | 218 | 90 | 231 | 107 | 375 | 369 | 413 | 165 | 88 | ||
| 428 | 266 | 257 | 130 | 142 | 383 | 193 | 103 | 73 | 75 | 316 | 191 | 105 | 334 | 194 | ||
| 122 | 352 | 83 | 18 | 4 | 405 | 312 | 104 | 31 | 34 | 33 | 250 | 172 | 37 | 422 | ||
| 439 | 408 | 310 | 258 | 397 | 252 | 123 | 398 | 356 | 269 | 262 | 395 | 21 | 367 | 368 | ||
| 355 | 146 | 178 | 400 | 321 | 278 | 152 | 86 | 182 | 173 | 184 | 69 | 51 | 111 | 71 | ||
| 32 | 350 | 333 | 433 | 79 | 412 | 417 | 418 | 391 | 290 | 421 | 112 | 341 | 166 | 420 | ||
| 416 | 167 | 125 | 240 | 168 | 62 | 237 | 128 | 55 | 354 | 129 | 141 | 343 | 284 | 303 | ||
| 158 | 24 | 23 | 279 | 272 | 39 | 373 | 338 | 297 | 274 | 254 | 208 | 281 | 15 | 362 | ||
| 330 | 119 | 325 | 207 | 196 | 183 | 372 | 171 | 113 | 275 | 374 | 138 | 410 | 288 | 255 | ||
| 271 | 188 | 197 | 213 | 336 | 211 | 61 | 423 | 137 | 63 | 385 | 70 | 7 | 66 | 26 | ||
| 8 | 329 | 276 | 386 | 151 | 77 | 30 | 64 | 426 | 425 | 289 | 169 | 357 | 227 | 363 | ||
| 380 | 156 | 109 | 224 | 339 | 283 | 241 | 387 | 78 | 222 | 411 | 384 | 306 | 265 | 256 | ||
| 132 | 337 | 228 | 377 | 314 | 57 | 133 | 43 | 331 | 315 | 72 | 110 | 108 | 332 | 115 | ||
| 342 | 181 | 65 | 260 | 219 | 202 | 236 | 20 | 402 | 381 | 379 | 203 | 177 | 267 | 264 | ||
| 232 | 217 | 96 | 378 | 320 | 221 | 293 | 431 | 419 | 359 | 432 | 414 | 396 | 434 | 429 | ||
| 427 | 435 | 415 | 229 | 442 | 438 | 437 | 443 | 424 |
Heuristics are criteria, methods, or principles for deciding which among several alternative courses of action promises to be the most effective in order to achieve some goal. They represent compromisses between two requirements: the need to make such criteria simple and, at the same time, the desire to see them distcriminate correctly between good and bad choices.É exatamente o caso das heurísticas implementadas. É necessário limitar a visinhança percorrida pela busca local
|
|
This document was generated using the LaTeX2HTML translator Version 99.2beta8 (1.43)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -no_navigation -split 0 -discard tp2-texto
The translation was initiated by Marcus Rocha on 2002-09-25
Trocar3Arestas(o1,d1,o2,d2,o3,d3) permanecem
válidos.